Miešanie kvapaliny v nádobe pri nízkej Reynolds číslo-v inertialess prostredí, nie je triviálne úloha. Vratné pohyby iba viesť k cyklom miešania a unmixing, tak kontinuálne otáčanie, ako sa používa v mnohých technologických aplikáciách, sa javí ako potrebné. Avšak, je tu ďalšie riešenie: pohyb stien v cyklickým spôsobom zaviesť geometrické fáze. Ukážeme využitie prietoku časopis nesúci ako model, ktorý takýto geometrický miešania je všeobecný nástroj pre použitie deformovateľné hranice, ktoré vracajú do rovnakej polohy miešať tekutinu pri nízkom počte Reynolds. Potom sme simulovať biologický príklad :. ukážeme, že miešanie v žalúdku funkcie kvôli "brušného fáze," peristaltické pohyb stien v cyklickej móde zavádza geometrické fáza, ktorá sa vyhne unmixing
Citácia: Arrieta J , Cartwright JHE, Gouillart E, Piro N, o Piro, Tuvalu i (2015) Geometrický Miešanie, peristaltika a geometrická fázy žalúdka. PLoS ONE 10 (7): e0130735. doi: 10,1371 /journal.pone.0130735
Editor: Christof Markus Aegerter, University of Zurich, Švajčiarsko
prijatá: 30.marca 2013; Prijaté: 23. mája 2015; Uverejnené: 08.07.2015
Copyright: © 2015 Arrieta et al. Toto je článok o otvorenej distribuovaný pod podmienkami Creative Commons Attribution licencie, ktorá umožňuje neobmedzené použitie, distribúciu a reprodukciu v nejakom médiu, za predpokladu, že pôvodný autor a zdroj sú pripísané
Financovanie: Autori prijímate finančnej podpory grantu FIS2010-22322-C02-01 /02 od ministerstva pre vedu a inovácie (MICINN) az "subprograma Ramón y Cajal" (IT). Platcovia mal žiadnu úlohu v dizajne štúdie, zber a analýzu dát, rozhodnutie publikovať, alebo prípravu rukopisu
Konkurenčné záujmy: .. Autori vyhlásili, že žiadne konkurenčné záujmy neexistujú
Úvod
Ako môže tekutina sa mieša pri nízkom počte Reynolds? Zmiešavanie sa zvyčajne vykonáva s miešadlom, otáčajúcim sa zariadenia vnútri kontajnera, ktorý produkuje komplex, chaotické prúdenie. Alternatívne, v prípade neexistencie miešadlom, otáčanie stien nádoby sa môže vykonávať zmiešavanie, ako sa vyskytuje v miešačke. Príležitostne sa však, miešanie sa pokus o cyklické deformáciu stien nádoby, ktorá neumožňuje pre čistý vzájomné posunutie zodpovedajúcich povrchov, situáciách, ktoré sa často vyskytujú ako v umelých zariadeniach a v živých organizmoch. Pri najnižších Reynoldsových čísel, podľa toho, čo je známe ako postupný podmienky prúdenia, zotrvačnosť kvapaliny je zanedbateľný, prúdenie tekutín je reverzibilná, a inverzie pohybu miešadla alebo steny vedie-up odchýlkam v dôsledku častice difúziou na unmixing, ako Taylor [1] a Heller [2] preukázaná. To by sa zdať, aby sa zabránilo používanie vratný pohyb miešať tekutinu pri nízkych Reynolds čísel; zdá sa, že povedie k stáleho cyklom miešania a unmixing. Vyvstáva teda otázka, ako cyklické zmeny v tvare nádob by mohlo viesť k účinnému miešania. Zoberme si prípad biologického toku dutiny: žalúdok. V žalúdku jedla a pitia sa miešajú do vytvorenia homogénnej tekutiny nazývaný tráveniny, ktorý je potom štiepený črevách. Žalúdočné miešanie sa vyrába tým, čo sa nazýva peristaltika podľa žalúdočnej steny sa pohybujú v rytmické spôsobom. Matematicky vyjadrené, tvar žalúdočnej steny prechádza uzavretý cyklus v priestore tvarov v priebehu každého cyklu peristaltika. Samozrejme iba tvar cyklov, ktoré nevyžadujú kumulatívne čistý posunutie medzi môžu byť považované za akékoľvek dve časti žalúdka. Ako je teda tento peristaltické pohyb žalúdočnej steny schopných produkovať miešanie, a to najmä u zvierat, u ktorých sa žalúdočné rozmery sú také, že kvapalina zotrvačná hmotnosť obsahu žalúdka je zanedbateľná?
Riešenie tohto hlavolamu zahŕňa pojem geometrická fázy Výsledky Journal tok ložisko Taylor [1] a Heller [2] použili toku Couette o nestlačiteľné tekutiny obsiahnutý medzi dvoma sústrednými valcami preukázať unmixing tekutiny vzhľadom k časovému reverzibility režimu Stokes. Tie ukázali, že po otočení vojne cez určitým uhlom, je možné, aby sa dospelo späť na počiatočný stav k unmix prietoku-obrátením tohto otáčania o rovnaký uhol s opačným znamienkom, a to aj keď je uhol je dostatočne, že veľká blob farbivá umiestneného v kvapaline bol zrejme dobre premieša. Vzhľadom k tomu, ako parametre v tomto zariadení polohy vonkajšie a vnútorné valcové steny nádoby špecifikovaných v tomto poradí s uhlami θ v kvapalnom systéme v režime Stokes, ako je tá naša, pretože zotrvačnosť je zanedbateľný pohyb je zo svojej podstaty vždy adiabatické a až vyvolané zmenou parametrov: polohami valcov. Preto každý výsledný fázový po kompletný cyklus v parametroch je geometrický fázy. V Heller-Taylor demonštrácii parameter slučka je veľmi jednoduchý: θ Všetky zero-area vzájomnej slučky sú stiahnuteľné, ale existuje mnoho ďalších prikladať konečnú oblasť. Pre získanie konečných priestor nerecipročné sťahovacie slučku možno, napríklad, prvé otočenie jeden valec a potom na druhú, potom sa obrátiť prvý a nakoniec reverznej druhej. Avšak, pre sústredných valcov prúdnice sú sústredné kruhy; ak sa pohybujeme jeden z valcov o uhol θ Zaznamenali sme, že od tej doby tok produkovaný recipročné cyklu hraníc vyvoláva mapy identity pre pozície každého prvku tekutiny v postupných cykloch, problém zmiešavanie tie nonreciprocal je úzko spätý do triedy dynamických systémov tvorených poruchami identity. Častice tekutina, ktorá na začiatku slučky je v polohe, dosiahne na konci toho istého slučky, jedinečné zodpovedajúceho bodu ( x Pozrime sa teraz dlhodobú tekutinu dynamika vyvolané opakovaným realizácie rovnakého stiahnuteľnom nerecipročné slučkou, ktorá indukuje danej mapy. Dynamika je popísaný opakované iterácie tejto mapy, ktorá sa chová ako stroboskopického mapy časovo periodické Hamiltonovho systému reprezentovaného nestlačiteľné prúdenie periodicky poháňaný pohybom stien. Pre malé slučky, mapa je malá odchýlka identity, ktorá môže byť považovaná za vykonávanie algoritmu Euler pre domnelé doba nepretržitého dynamického systému definuje tento rozrušenie. Preto v 2D očakávame, že iterácie mapy bude pozorne sledovať trajektórie tejto 2D priebežného systému, ktorý je integrovateľné. Preto bude kvapalných častíc mix veľmi pomaly vo vesmíre: to je, tak povediac, zmiešavanie tekutín "kvázi-statické". To je dobre zobrazené na obr 2 (a), kde aj na štvorcovú slučkou tvorenú s hodnotami, ako sú veľké ako θ Vzhľadom k tomu, geometrické fáza a zodpovedajúce rozrušenie z identity zvýšenie mapa, bývalý argument, začína zlyhávať [19]. Viac chaotické 2D-area zachovanie mapa vynorí as ním aj zodpovedajúci priestor na plnenie úplne chaotické trajektórie. KAM ostrovy typicky bude menšie a menšie, ako charakteristické hodnoty zvýšenie geometrického fázy. Ako vidíme na obrázku 2 (b) za θ Na obrázku 2 (d) -2 (f) ukážeme zodpovedajúce distribúcia geometrického fázy nad domény. Hodnota geometrického fázy v danej východiskovej polohe, získané z hľadiska konečného uhla mínus počiatočné uhol v bipolárnych súradníc (pozri oddiel materiály a metódy pre ďalšie podrobnosti) po jednom priechodu, Φ = ξ Tok časopis ložiska je len jedna do skupiny tokov, ktoré zobrazujú geometrické miešania. V otvorených tokov, jeden má inštancie, ako sú dobre známe Purcell plavca, ktoré možno považovať za prevádzky prostredníctvom geometrického fáze. Ďalšie uzavretý tok, ktorý bol študovaný na počiatku chaotickej advekčního je obdĺžniková dutina toku, v ktorom jeden alebo viac zo stien kvapalinou naplnenou obdĺžnikový kontajner sa môže pohybovať, je nastavený ako dopravné pásy [15, 20]. Rovnako ako v prípade predchádzajúcich štúdií časopise ložisko, tieto zmiešavacie protokoly znamenať kumulatívnu relatívnej posunutie stien nádoby. Avšak, rovnako ako v prípade časopisu ložiska možno zaviesť geometrický fázy tým, že vráti všetky steny, aby ich počiatočné vzájomnej polohy po slučke v parametroch. Všeobecnejšie povedané, je možné uvažovať o tokov indukovaných kontajnera, v ktorom steny nepohybujú ako tuhá telesá, ale namiesto toho sa môže deformovať v pozdĺžnom smere a /alebo tangenciálne pozdĺž nonreciprocal cyklu, za účelom výroby účinného miešania. Napríklad, jeden by mohol zvažovať prípad pružného vrecka s tekutinu a vystavený pôsobeniu periodickej stláčanie-distenčního sekvenciu okolo jedného zo svojich úsekov s kompenzačným distenčního stlačenia akciu okolo druhého. Tento cyklus by zjavne prinútiť tok vratný nevhodné pre efektívne miešanie, ale zase by mohla byť vykonaná geometrická fázy existovať, ak to priestorovo stacionárne usporiadanie bolo nahradené jediným, ktorý sa šíri pozdĺž osi vrecka. žalúdok je biologický príklad takého prúdu dutiny [21, 22]. Ľudský žalúdok je silná svalová nádoba medzi pažerákom a tenkého čreva. To nie je len zásobné komora pre potraviny, ale aj mixér, kde sa pripravuje chymus. Ľudský žalúdok má objem L Žalúdočné miešanie priniesla peristaltické waves- priečny cestovanie vlny kontrakcí-, ktoré šíria pozdĺž žalúdočnej steny u niektorých 2,5 mm s -1. Sú začali približne každých 20 sekúnd, a trvať asi 60 ov prejsť dĺžku žalúdka, takže 2-3 vlny sú prítomné naraz, kým v priemere o šírke žalúdka ako vlna prejde je 0,6 násobok jeho normálna šírka [21 , 22]. Máme teda ich rýchlosť c pre zobrazenie účinky tejto fázy sme skonštruovali minimálny model žalúdka prechádza peristaltiky, ako je načrtnutá na obr 4 (a) a ďalej podrobne popísané v časti materiály a metódy. úmyselne sme znížili geometrické, dynamické a funkčné zložitosti žalúdka a modelovať 2D časť rúrkového žalúdka jednotným polomerom, s utesnenými pyloru a pažeráka ventily, zamerať sa na rolu peristaltické kontrakcie môže hrať v miešaniu v rámci uzavretého inertialess dutina. Podobne sme liečili tráveniny ako newtonovskej kvapaliny, pričom zložitosť spojené s viskoelasticity pre ďalšie práce, ako je existencia alebo nie geometrického miešania v žalúdku je nezávislá na viskoelastických vlastností tráveniny. Podobný model bol použitý v [4, 26] na posúdenie dopravu peristaltické čerpanie v nekonečných štíhlych trubiek. V našom modeli peristaltické vlny deformuje horná a dolná hranica symetrické dutiny pomerom strán π Považujeme za miešania pasívneho skalárna, ktorého prvé priestorové rozloženie na t získať geometrické fázy integráciou trajektórie pasívne skaláry v priebehu jedného celého cyklu, s rovnomerne rozdelené počiatočnými podmienkami v doméne [0, 2 π žalúdočné kontrakcie, ktoré zodpovedajú stojaté vlny sú blízky nulové oblasti vzájomného slučky. Ako sme predpokladali pre prípad časopis ložiská, recipročné slučky indukuje tok, ktorý nevytvára žiadne miešanie. To je znázornené na obr.5 (b), kde poľa koncentrácia po 20 cykloch hranice deformačných ako stojaté vlny je zobrazený. Vzhľadom k tomu, indukovanej geometrický fáza je null, miešanie je riadený len (pomaly) difúzie. Význam geometrického miešanie v žalúdku môže byť zrejmé s odkazom na prípady, v ktorých je narušená. Žalúdok je ako srdce, s elektrickou aktivitou z regiónu kardiostimulátora stimulujúce oscilácie; V tomto prípade je cestovanie vlny peristaltiky. Ak je tento systém nepracuje správne, môže byť gastroparézy alebo žalúdočné fibrilácia [31, 32], v ktorom peristaltické vlny stanú neusporiadaná. Sme vytvorili také disordered deformáciou podľa interspersing peristaltické vlny, ktorých šírenie rýchlosti c porovnať stupeň miešanie vo všetkých troch prípadoch sú tu považované za (peristaltiku (pw), stacionárne (SW) a náhodné (RW) vlny), sme sa vypočíta pre každý cyklus rozptyl priestorové pole koncentrácie [33, 34], σ V súhrne sme zaviedli pojem geometrického miešania, v ktorom zmiešavanie vzniká v dôsledku geometrického fázy vyvolanej sťahovacie nerecipročné cyklu v súlade s parametrami, ktoré definujú tvar nádoby. Ukazuje sa, že zmiešavacie účinnosť odhadnúť z preťahovanie materiálu liniek je zhruba úmerný geometrickému fázy. Miešanie v zodpovedajúcich tokov môže byť tiež považovaná za výsledok chaos vznikajúce pri mapovaní opisuje pohyb tekutinových prvkov v priebehu jedného cyklu. Keď je cyklus recipročné, je táto mapa totožnosť a malá odchýlka od reciprocity zodpovedá malej odchode z mapy identity. Chaotické vlastnosti máp susedných identity boli málo študované v minulosti. Oni tiež vznikajú v celkom inom kontexte numerických integračných metód obyčajných diferenciálnych rovníc v limite, kde je veľkosť kroku blíži nule [19]. Naše výsledky sú preto tiež relevantné pre charakterizáciu chaosu v tejto triede systémov. A konečne, sme ukázali, že taký geometrický fáza-the "brucho fáza" [35] môžu byť s nájsť v žalúdky, kde Re Hotel < 1. Podporné informácie Journal tok ložisko Tok časopis ložiská boli široko využívaná na štúdium proces miešania v laminárnom prúdení. Obrázok 6 ukazuje nákres usporiadania tu študovanej. Vonkajší valec s polomerom R Vzhľadom k linearity problému riešenie pre funkciu prúdu môže byť písaný ako (1) kde ψ Akonáhle je prietok vyhodnotená, boli získané trajektórie častíc integrácie (10) (11) začlenenie rovníc (10) a (11) bol vykonáva pomocou štvrtého poriadku schémy Runge-Kutta. Potom, čo jeden úplný cyklus, obaja vojne skončiť na svojom pôvodnom mieste, zatiaľ čo častice odchýlenie od počiatočnej polohy ( ξ
. Geometrický fázy [3] je príkladom anholonomy: zlyhanie systémových premenných vrátiť do svojej pôvodnej hodnoty po uzavretom okruhu v parametroch. V tomto liste navrhujeme to, čo nazývame geometrické mixovanie: použitie geometrického fáza zavedené nonreciprocal cyklovanie deformovateľnej hranice kontajnera ako nástroj pre miešanie tekutín pri nízkom počte Reynolds. Ako príklad, ako tento proces vedie k účinnému miešaniu, použijeme známy dvojrozmernej zmiešavač založené na prietoku čape ložiska avšak s výhradou oveľa-menej-študovala otáčania protokol, ktorý spĺňa geometrické obmedzenia cyklických okrajových deformácií. Konečne sme sa ukázať, že peristaltiku okrem svojho príspevku k dôležitým biologických funkcií, ako je doprava tekutín v rámci jednotlivých lineárnych orgánov [4, 5] alebo signalizačné po celom komplexných biologických [6] štruktúr, plní svoju ústrednú úlohu v žalúdku miešaní a trávenie [7-9] prevádzkovaním vďaka geometrickému fázu v žalúdku.
1 a θ
2 z danej štartovanie bod, geometrická fáza by mohli vzniknúť z riadenia tohto systému okolo slučky v parametrickom priestore.
1 prvého zvyšuje určitú sumu a potom sa znižuje rovnakú sumu, zatiaľ čo θ
2 zostáva pevná. Táto slučka obopína žiadny priestor, a vratnosť zaisťuje, že fáza je nulová. Zložitejšie zero-area
slučiek môže byť postavená tým, že kombinuje v rade ľubovoľnej dvojice vzájomných otáčok oboch valcov, a oni tiež viesť k nulovej fáze. Budeme nazývať tieto konštrukty recipročných cyklov
. Aby bolo možné zvážiť menej triviálne slučky, môžeme najprv poznamenať, že parameter priestor je homotopická na 2-torus. Slučky na takom priestore môže byť klasifikované podľa počtu plných otočenie, že oba parametre sa hromadia pozdĺž slučky. Všimnite si tiež, že vzájomné otáčanie 2 π
medzi stenami prináša kontajner do pôvodného stavu, s výnimkou globálne otáčania. Vzhľadom k tomu, máme záujem o tvare slučiek, ktoré možno dosiahnuť bez čisté kumulatívne posunutie povrchov nádob, musíme vziať do úvahy iba triedu typu 0 alebo stiahnuteľnom
(do bodu) slučky.
, sledovacie častice sa bude pohybovať po kružnici o uhol, ktorý závisí len na θ
. Potom je zrejmé, že kumulatívny účinok pohybujúce sa jeden valec θ
1, potom druhý θ
2, potom prvý - θ
1, a druhá - θ
2, je vrátiť častice do pôvodnej polohy: nie je žiadna geometrická fázy, a unmixing stále dochádza. Ale ak budeme meniť nastavenie Heller-Taylor a vyrovnanie vnútorné valec, dôjdeme na to, čo je známe ako tok časopis ložiská. O zavedení excentricitu ɛ
medzi valcami, tento tok má radiálne zložku. V limitným plazivej-flow, Navier-Stokes rovnice pre prúdenie časopis nesúceho znížiť na lineárnej biharmonic jeden, ∇ 4 ψ
= 0, pre funkciu prúdu, ψ
, a môžeme modelovať tento systém využívajúci analytické riešenia (pozri [10-12] a časť materiály a metódy pre ďalšie podrobnosti). Ak teraz vykonať parametrov slučky sekvencií otáčok je uvedené vyššie, dostaneme späť do nášho východzieho bodu z hľadiska polôh oboch valcov, takže je možná prekvapujúce, že vnútorná kvapalina sa nevráti do jeho počiatočný stav. Ukazujeme prítomnosť tohto geometrického fázy na obr 1, v ktorom je uvedený príklad trajektórie častice kvapaliny, ako sú steny sú poháňané prostredníctvom nonreciprocal zmršťovacie slučky. prietok Journal ložiská bol veľa študoval v minulosti [13-16], ale nikdy sa zmrštiteľných slučiek tak, aby táto geometrická efekt nebol nikdy zdôraznený. Táto malá zmena protocolary v dobre zavedenom prúde má, však podstatný vplyv na dynamiku tekutín, ako popisujeme nižšie.
', z China "), ktorá je funkcia one-to-one ( x
', z China') = G [( x
z China)] z počiatočnej jedna. Pre homogénne kvapaliny, G musia byť spojitá a diferencovateľná, zatiaľ čo nestlačiteľnosti znamená, že G zachováva oblasť ľubovoľnej domény bodov. Inými slovami, nestlačiteľné znamená Hamiltonovské dynamiku pre kvapalných častíc, a mapa sa, že táto dynamika vyvoláva v jednej slučke je oblasť konzervovanie. Pre stiahnuteľnom nulového priestoru slučky mapa je jednoducho identity; každá častica končí v polohe, v ktorej sa začal. Z tohto dôvodu, konečný-oblasť slučky indukuje všeobecne konečný odchýlka od mapy identity a charakteristickou hodnotou geometrického fázy dáva odhad rozsahu tejto odchýlky. Vzhľadom k tomu, druhovo geometrických zvyšuje fázy o ploche slučky, pre malé slučky mape je malá odchýlka od identity, zatiaľ čo slučky väčšiu plochu vyvolať väčší odchýlky.
= π
/2 pozíciami kvapalných častíc po sebe idúcich očiek hladko posun pozdĺž uzavretej krivky, ktoré sú trajektórie priebežných dynamiky. Trajektórie sú zložené zo segmentov, ktoré takmer nasledujú integrovateľné trajektórie 2D prietoku (približne určiť ako mapy Euler), pokiaľ nedosiahne oblasť rozsiahle fáze, kde sa vyskytujú chaos a heteroclinic spleti. Tam častice prejde do iného kvázi-integrable trajektóriu, až sa opäť dosiahne oblasti veľkých fázy. V typickom Hamiltonovho chaose (štandardná mapa, napríklad) mapa nie je odchýlka totožnosti, ale odchýlka od lineárneho strihu (tj kanonickej akčné uhla dynamických veličín (I, φ
) Nasledujúce I
'= I
, φ
' = φ
+ I
"), čo bolo dôvodom pre toto správanie nie je normálne vidieť [17, 18]. Štruktúra chaosu v tejto triede dynamiky bola značne prehliadaná v literatúre, a súčasný výskum otvára novú cestu k pochopeniu tohto problému spojeného.
= 2 π
RADIANS, a ešte viac tak obr 2 (c) pre θ
= 4 π
radiánov, po 10000 cykloch častice kvapaliny sa vzťahuje väčšina z oblasti má k dispozícii medzi dvoma valcami. To je miešanie kvapaliny vyvolané úplne geometrickým fázy; ich môžeme nazývať geometrický zmiešavanie. Geometrické miešanie preto vytvára chaotické najmä advekcia [15], rovnako ako klasický časopis nesúci protokolu.
f
- ξ
aj
, je znázornená na farebnej škále intenzít červené (pozitívne) a modrej (negatívne). Všimnite si, že fáza klesne na nulu na steny, ako to musí byť, ale silne mení cez domény. Najmä v prípade parametrov θ
= 2 π
RADIANS (obr 2 (e)), vidíme vývoj jazyka vysokých hodnôt geometrického fázy v jednom zmysle interpenetrujících oblasť vysokých hodnôt fázy v opačnom zmysle. Trajektórie vynesené na obr 1, ukazuje pôvod jazyka; fluidné častice, ktoré sú advected do blízkosti vnútorného valca o prvý θ
1 krok sa potom advected k výrazne odlišné hodnoty r
podľa vnútorného valca. Výsledkom je, že sa častice kvapaliny sa nachádza v úplne inom Streamline z prvého kroku, kedy sa začne otáčať dozadu vonkajšej valec. Ako možno očakávať, pre menšie hodnoty parametrov tento jazyk nie je prítomné (obr 2 (d)). Pri ešte vyšších hodnotách θ
, na druhej strane, (viď obr 2 (f)) je jazyk obteká dvakrát kolo vo veľmi zložito. Na obr 2 (g) (i) -2 ukazujeme vynesením vývoj radu počiatočných podmienok, ako je geometrická fáza súvisiace s dynamickou štruktúru toku. Obrázok 2 (g), za θ
= π
/2 radiánov, ukazuje, že keď tento jazyk je chýba, úsečka sotva sa vyvíja; prietok je takmer reverzibilné. Segmenty čiary na obr 2 (h) a 2 (i), na θ
= 2 π stroje a 4 π
radiánoch, na druhej strane, vykazujú mnoho preťahovanie vyvolané týmto jazykom veľké geometrické fázy. Pre demonštráciu tohto efektu geometrické fázy na tok podrobnejšie na obr 3 (b) sme plot dĺžku úsečky po jednom cykle proti uhlu natočenia. Pozoruhodným aspektom tohto grafu je, že zobrazuje plošiny oddelené období rýchleho rastu. Porovnanie s obr 2 (d) -2 (f) ukazuje, že sa jedná o prienik jazykom veľkej hodnoty geometrického fázy počas tohto úsečky, ktorá vyvoláva rozťahovanie. Jazyk preniká prvýkrát pred θ
= 2 π
, a potom druhýkrát pred θ
= 4 π
, tak produkovať dva skoky; medzi týmito mostíky vývoj úsečky je oveľa pomalší. Pre daný nákladov na energiu, ktorá škáluje s celkovým nepodpísaného posunutie stien, geometrické miešanie je teda účinnejší pre veľkú hodnotu θ
.
peristaltike zmiešavanie
3 z približne 330 ml, pričom sa viskozita μ
z tráveniny je rádovo 1 Pa s, jeho hustota je <ρ br> ≈ 10 3 kg m -3 a maximálnej rýchlosti prúdenia v
pozorované sa pohybujú v rozmedzí 2,5 - 7,5 mm s -1 [21]. Z týchto údajov môžeme odhadnúť počet Reynolds Re
= ρVL
/ μ
ležať v rozmedzí 0,2-0,5. Môžeme teda konštatovať, že v ľudskom zotrvačnosti žalúdočnej tekutiny má iba obmedzený význam, a v každom menšom zvierati to bude bezvýznamný. Berieme na vedomie, že predchádzajúce práce na žalúdočné miešanie bola väčšinou považovaná za prípad inerciálnych príspevkov [21, 23, 24], pre ktoré neplatia dynamické obmedzenia tu popisované.
= 2,5 mm s -1, frekvencia ω
= 0,05 Hz, a odtiaľ vlnová dĺžka λ
= c
/ omega
= 5 cm a ich amplitúdy b
= 1/2 x 0,6 L
≈ 2 cm. Tieto vlny núti žalúdka cez nonreciprocal slučkou v priestore tvarov, v dôsledku ktorého sa očakáva, geometrické miešania. Jeden môže dať hrubý odhad veľkosti očakávané geometrického fáze s využitím výsledkov získaných pre ďalší problém geometrické fáza: to low-Reynolds-počet mikroorganizmov plávanie. Mnoho baktérií plávať deformáciou ich tela rovnakým spôsobom ako peristaltické vlny žalúdka a ich rýchlosť je dobre odhadnúť na základe modelovania také deformácie ako rovinné vlny [25]. Podobné výpočty pre žalúdka činí rýchlosť prúdenia vyvolaného peristaltické vlny V
= πc
( b
/ λ
) 2 , ktorý vychádza na približne 1 mm s -1, odkiaľ sa očakáva, že posunutie asi 6 cm na peristaltické cyklus, alebo s ohľadom na kruhový žalúdok polomere L, geometrické fáza rádovo 2 radiánoch.
podľa z China w
( x
t
) = 1+ b
sin ( kx
- ? t
) v ( x
z China) -coordinate systém. Prietok v dutine sa získa integráciou rovnice Stokesových pre rýchlostného poľa ( u
, v
) so zodpovedajúcimi okrajovými podmienkami pre peristaltické vlny na hornej hranici, u
= 0 a v
= ∂ z China w
/∂ t
na z China = z China w
( x
t
), a symetria okrajových podmienok na z China = 0 . Bočné steny deformuje zvisle tak, aby zodpovedala vertikálnu rýchlosť peristaltické vlny na x
= 0 a x
= 2 π
. Na obr 4 (a) čierne pevné čiary predstavujú prúdnice indukovaného tekutiny pohybu vnútri dutiny v dôsledku peristaltické vlny. Obrys sprisahania zodpovedá časovo Pre priemerné rýchlosti cez jeden celý peristaltické cyklu. Oblasti maximálnej priemernej rýchlosti sú v blízkosti osi symetrie, zatiaľ čo pri stene priemerná rýchlosť je nula a nie je priemerný pohyb je produkovaný.
= 0 je daná rozmazané kroku (, ako je znázornené na mape obrysu na obr 4 (b). získa sa časový vývoj tejto priestorovej koncentrácie integráciu prúdenie tepla, difúzna rovnica pre charakteristické číslo Péclet, Pe
= cλ
/ D
chymus
zástupcu miešacieho procesu v žalúdku. Vzhľadom k tomu, charakteristický difuzivita tráveniny je, nanajvýš o poradí molekulárnej difúzie veľkých makromolekúl D
chymus
≤ 10 -6 cm
2 / s
Pe Úvod »1 a advective príspevky dominovať miešacej proces obr. 4 (c) reprezentuje priestorovú koncentráciu pasívne skalárna χ
po 20 cykloch peristaltické (teda po rescaled čas T
= t
/ T
* = 20, kde T
* predstavuje periódy cyklu) pre Pe
= 15 x 10 3. Prúd indukovaný peristaltika hromadia konečnú geometrickou fáze po každom cykle, tekutinových prvkov sa pretiahla a zložené a, v dôsledku toho, tenké vlákna sú vytvorené, ktoré uľahčujú zmiešavacie vnútri dutiny.
] × [0, z China w
( x
0)]. Euklidovská vzdialenosť medzi počiatočný a konečný polohe po jednom cykle poskytuje odhad geometrického fázy. Obrysy na obr 4 (d) predstavujú geometrické fázu systému. Je vidieť, že maximálna posuny sú pozorované v strednej oblasti dutiny, kde sú vytvorené vlákna. Všimnite si, že regióny na obr 4 (d) s malými posunutie zodpovedajú oblastiam, ktoré zostávajú Unmixed na obrázku 4 (c). Tak, a to aj napriek stály polomer dutiny v našom minimálnom geometrického modelu, miešanie nie je priestorovo rovnomerné. Regióny v centrálnej časti dutiny tvoria tenké vlákna, ktoré zlepšujú miešanie, zatiaľ čo regióny v blízkosti bočnej a na horných stenách zostali po 20 cykloch takmer nezmiešané. Aj ďalšie nehomogenity sa očakáva, že pre vernejšie geometriou, sa mení stredný priemer steny [27], špecifická časovanie otváranie a zatváranie pyloru s peristaltiky [28] a interakcie medzi fundusu /srdcovej oblasti žalúdka [29], všetko o ktorých je známe, funkciu pre miešanie v žalúdku [30].
sú vybrané náhodne z rovnomerného rozloženia nulovou strednou hodnotou. Skalárne pole χ
zostáva takmer Unmixed v porovnaní s peristaltickým prípade po ekvivalentnú dobu integrácie, pričom sa zmes mieša väčšinou riadený opäť pomalou difúziou (obrázok 5 (c)). Teda, v našich podmienkach, je zlá miešanie, alebo bez nutnosti miešania v gastroparézy, pretože nie je slučka okolo priestoru formy, takže žiadny priemer geometrickej fázy, a namiesto toho náhodné peristaltické vlny vyvolať iba miešania a unmixing.
= <( χ
- < χ
>) 2> 1/2, kde <> označuje priestorový priemer. Obrázok 5 (a) predstavuje vývoj σ
s počtom cyklov. Vyplýva z nej, vyššia účinnosť miešanie realizovaný v peristaltiky podľa geometrického miešaním.
Diskusia
Mimo
rotuje s uhlovou rýchlosťou W z China, zatiaľ čo vnútorného valca s polomerom R
v
otáča s uhlovou rýchlosťou W v
. Výstrednosť vnútorného valca je daný ɛ
. V limitnom prípade viskózne sily sú zanedbateľné, je výsledný prúd sa získa integráciou biharmonic rovnice pre funkciu prúdu ∇ 4 ψ
= 0 so zodpovedajúcimi okrajovými podmienkami na stenách valcov.
z China je riešením pre funkciu prúdu toku vyvolaného vonkajšieho valca, vzhľadom k tomu, ψ
v
zodpovedá riešení funkcie prúdu toku vyvolaného vnútorného valca. Uhol krytá vojne behom jedného cyklu závisí na jeho uhlovej rýchlosti podľa odseku (2), kde sa subindex aj
označuje vonkajšie alebo vnútorné valec a T
* predstavuje obdobie cyklu , Vzhľadom k tomu, v simuláciách uvažovaných v tomto dokumente uhlová rýchlosť valcov je konštantná, Θ aj
= T
* Ω i
. Tento tok pripúšťa presné riešenie [11] pre funkciu prúdu, keď je problém napísaný v bipolárnych súradníc ( ξ
η
). Pravouhlých súradníc ( x
z China) možno získať podľa odseku (3), kde (4) Na [11] riešenie pre vnútorné a vonkajšie prúdu funkcia je daná vzťahom (5 ) kde H
= b
/( c
2+ s
2) 1/2, s s
= sin ξ
hriechu η stroje a c
= cosξ
cos η
- 1. Okrem toho, (6) (7) a (8) (9) withwhere ξ
v
a ξ
von
predstavujú povrchy vnútorných a vonkajších valcov, respektíve, a Δ ,, Δ *, h
1, h
2, ..., h
8 sú dané
aj
, η
i
) sú umiestnené na ( ξ
f
η
f
).
 Ústna voda ovplyvňuje účinky cvičenia
Ústna voda ovplyvňuje účinky cvičenia
 Staroveké mikrobiómy primátov môžu poskytnúť viac informácií o vývoji človeka
Staroveké mikrobiómy primátov môžu poskytnúť viac informácií o vývoji človeka
 Majú ženy väčšiu pravdepodobnosť vzniku dlhého COVID -u?
Majú ženy väčšiu pravdepodobnosť vzniku dlhého COVID -u?
 Štúdia objasňuje príčiny oslabujúcej bolesti čriev
Štúdia objasňuje príčiny oslabujúcej bolesti čriev
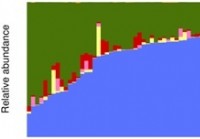 Štúdia opisuje počiatočnú východiskovú databázu zdravých črevných mikrobiómov a profil početnosti
Štúdia opisuje počiatočnú východiskovú databázu zdravých črevných mikrobiómov a profil početnosti
 Zmena mikrobiómu horných dýchacích ciest u detí súvisiaca s citlivosťou na SARS-CoV-2
Zmena mikrobiómu horných dýchacích ciest u detí súvisiaca s citlivosťou na SARS-CoV-2
 Obmedzený zápal čriev pri COVID-19
Ochorenie COVID-19 je charakterizované predovšetkým horúčkou, kašeľ, a respiračné symptómy. Avšak, Teraz je tiež známe, že ovplyvňuje mnoho ďalších orgánov, hlavne črevo. V skutočnosti, až 60% hospita
Obmedzený zápal čriev pri COVID-19
Ochorenie COVID-19 je charakterizované predovšetkým horúčkou, kašeľ, a respiračné symptómy. Avšak, Teraz je tiež známe, že ovplyvňuje mnoho ďalších orgánov, hlavne črevo. V skutočnosti, až 60% hospita
 Črevný mikrobióm je realitou aj v živote plodu
Štúdia publikovaná v Journal of Clinical Investigation ukazuje, že u myší aj u ľudí fetálne črevo má svoj vlastný mikrobióm, čo je pravdepodobne odvodené priamo z materského organizmu. Tomu sa hov
Črevný mikrobióm je realitou aj v živote plodu
Štúdia publikovaná v Journal of Clinical Investigation ukazuje, že u myší aj u ľudí fetálne črevo má svoj vlastný mikrobióm, čo je pravdepodobne odvodené priamo z materského organizmu. Tomu sa hov
 Zmena mikrobiómu horných dýchacích ciest u detí súvisiaca s citlivosťou na SARS-CoV-2
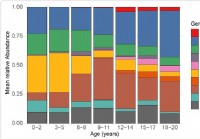
Vedci testovali nazofaryngeálny mikrobióm detí do 21 rokov a zistili, že sa mikrobióm mení s vekom. Špecifické baktérie, ktorých početnosť sa tiež mení s vekom, sú spojené s citlivosťou a závažnosťou
Zmena mikrobiómu horných dýchacích ciest u detí súvisiaca s citlivosťou na SARS-CoV-2
Vedci testovali nazofaryngeálny mikrobióm detí do 21 rokov a zistili, že sa mikrobióm mení s vekom. Špecifické baktérie, ktorých početnosť sa tiež mení s vekom, sú spojené s citlivosťou a závažnosťou