Финансирование: Авторы выражают благодарность финансовой поддержке гранта FIS2010-22322-C02-01 /02 от Министерства науки и инноваций (MICINN) и от "subprograma Рамон Кахаль" (IT). Доноры не играет никакой роли в дизайн исследования, сбора и анализа данных, решение о публикации или подготовки рукописи
<р> Конкурирующие интересы:.. Авторы заявили, что не существует никаких конкурирующих интересов
Введение Результаты Журнал подшипник потока Все нулевой зоны взаимные петли стягиваемы, но есть еще много ограждающих конечную площадь. Для получения конечной зоны ответственности невзаимный стягиваемую цикла мы можем, например, вращать первый один цилиндр, а затем другой, потом обратно первым, и, наконец, обратная другой. Тем не менее, для концентрических цилиндров линий тока представляют собой концентрические окружности; если мы перемещаем один из цилиндров на угол θ Для того, чтобы показать влияние этой фазы, мы построили минимальную модель желудка проходит перистальтики, как было отмечено на фиг.4 (а) и более подробно в Материалы и методы секции. Мы намеренно сократили геометрические, динамические и функциональные сложности желудка и моделировать 2D сечение трубчатого желудка равномерного радиуса, с герметизированными привратника и пищеводу клапанов, чтобы сосредоточить внимание на роли перистальтических сокращений могут играть при смешивании в закрытой безынерционной полость. Кроме того, мы рассматривали химуса как ньютоновской жидкости, оставляя сложности, связанные с вязкоупругости для будущей работы, как наличие или отсутствие геометрического смешивания в желудке не зависит от вязкоупругих свойств химуса. Аналогичная модель была использована в работах [4, 26] для оценки транспорта по перистальтической накачке в бесконечных тонких трубок. В нашей модели перистальтический волна деформирует верхние и нижние границы симметричного полости соотношением сторон π Таким образом, мы ввели понятие геометрического перемешивания, в котором перемешивание возникает как следствие геометрической фазы, индуцированной стягиваемое невзаимные цикл в параметрах, определяющих форму контейнера. Оказывается, что эффективность смешения оценивается от растяжения материальных линий примерно пропорционально геометрической фазы. Смешивание в соответствующих потоках можно также рассматривать как результат хаоса, возникающие при отображении, описывающее движение элементов жидкости в течение одного цикла. Когда цикл взаимна, это отображение является тождественным и небольшой отход от взаимности соответствует небольшой отход от тождественного отображения. Хаотические свойства карты соседних идентичности были слабо изучены в прошлом. Они также возникают в совершенно ином контексте численных методов интегрирования обыкновенных дифференциальных уравнений в пределе, когда размер шага стремится к нулю [19]. Наши результаты, таким образом, также имеет отношение к характеристике хаоса в этом классе систем. И, наконец, мы показали, что такая геометрическая фаза-«фаза живота» [35] -Может быть найдены в желудках животных, где Re Поддержка Информация Журнал потока подшипник в силу линейности задачи решение для функции тока можно записать в виде (1) где ψ
<р> Как может быть смешано жидкости при низких числах Рейнольдса? Такое смешивание обычно выполняется с помощью мешалки, поворотное устройство, внутри контейнера, который производит сложное, хаотическое поток. В качестве альтернативы, в случае отсутствия мешалки, вращение стенок контейнера сами могут выполнять перемешивание, как это происходит в бетономешалке. В тех случаях, однако, смешивание попытка циклической деформации стенок контейнера, что не допускает чистого относительного смещения соответствующих поверхностей, ситуаций, которые часто возникают как в искусственных устройствах и в живых организмах. При самых низких числах Рейнольдса, при том, что известно, как ползучий условия потока, инерция жидкости незначителен, поток текучей среды является обратимым, и инверсия движения мешалки или стенок приводит вверх к возмущениям вследствие частицы диффузии в расслоении, а Тейлор [1] и Геллер [2] было показано. Это, казалось бы, исключает использование возвратно-поступательное движение для перемешивания жидкости при малых числах Рейнольдса; казалось бы привести к бессрочным циклов смешивания и расслоении. Тогда возникает вопрос о том, как циклические изменения в форме контейнеров может привести к эффективному перемешиванию. Рассмотрим случай биологического потока полости: желудок. В желудке пища и питье, смешивают с образованием однородной жидкости называют химуса, который затем усваиваются кишечником. Желудочный смешивание производится, что называется перистальтика: по стенкам желудка, движущихся в ритмической моды. В математических терминах, форма стенок желудка проходит замкнутый цикл в пространстве форм во время каждого цикла перистальтики. Очевидно, что только формируют циклы, которые не требуют кумулятивный чистый сдвиг между любыми двумя секции желудка могут быть рассмотрены. Как же это перистальтику желудка стенок, способных производить смешивание, особенно у животных, у которых размеры желудка таковы, что инерция жидкости содержимого желудка ничтожно мало?
<Р> Решение этой головоломке включает в себя концепцию геометрическая фаза
. Геометрическая фаза [3] является примером anholonomy: сбой системных переменных для возврата к исходным значениям после того, как по замкнутому контуру в параметрах. В этом письме мы предлагаем то, что мы называем геометрическое смешивание: использование геометрической фазы, введенной невзаимного круговорот деформируемых границ контейнера в качестве инструмента для перемешивания жидкости при низких числах Рейнольдса. В качестве примера, как этот процесс приводит к эффективному перемешиванию, мы используем хорошо известную двухмерную смеситель, основанный на потоке цапфы но при условии гораздо менее изученной протокол вращения, который удовлетворяет геометрических ограничений циклических граничных деформаций. Мы, наконец, показать, что перистальтику, помимо своего вклада в важных биологических функций, таких как транспортировка текучих сред внутри отдельных трубчатых органов [4, 5] или сигнализации на протяжении сложных биологических структур [6], выполняет свою центральную роль в желудочном перемешивания и пищеварения [7-9] при работе благодаря геометрической фазы в желудке.
<р> Тейлор [1] и Геллер [2] использовали Куэтта несжимаемой жидкости заключенной между двумя концентрическими цилиндрами, чтобы продемонстрировать несмешивание жидкости вследствие обратимостью во времени режима Стокса. Они показали, что после того, как вращающиеся цилиндры через определенный угол, то можно прийти обратно в исходное состояние, чтобы unmix Проточный путем изменения этой поворот на тот же угол с противоположным знаком, даже когда угол достаточно того, что большая капля красителя, помещенного в жидкости было, по-видимому хорошо перемешана. Учитывая в качестве параметров в этом устройстве позиции внешних и внутренних цилиндрических стенок контейнера, указанных соответственно с углами θ
<югу> 1 и θ
<югу> 2 из данного пуска точка, геометрическая фаза может возникнуть от вождения этой системы вокруг контура в пространстве параметров.
<р> в системе жидкости в режиме Стокса, как наша, как инерция ничтожна движение по определению всегда адиабатическим и только индуцированное изменением параметров: позиции цилиндров. Таким образом, в результате чего любой фазы после полного цикла в параметрах является геометрической фазы. В демонстрации Heller-Тейлора петля параметр очень прост: θ
<югу> 1 первый увеличивает определенное количество, а затем уменьшается и ту же сумму, в то время как θ
<суб> 2 остается неподвижным. Этот цикл не охватывает ни одна область, и обратимость гарантирует, что фаза равна нулю. Более сложные нулевой область
петли могут быть построены путем объединения в последовательности произвольных пар взаимных вращений обоих цилиндров, и они также приводят к нулевой фазе. Мы будем называть эти конструкции обратные циклы
. Для того чтобы рассмотреть менее тривиальных петель, мы можем сначала заметим, что пространство параметров гомотопно 2-тора. Петлями на таком пространстве могут быть классифицированы в соответствии с количеством полных витков, что оба параметра накапливаются вдоль петли. Отметим также, что относительное вращение 2 π
между стенками приводит контейнера к исходной конфигурации для глобального вращения, за исключением. Так как мы заинтересованы в циклах формы, которые могут быть достигнуты без чистого кумулятивного смещения поверхностей контейнеров, нам нужно рассмотреть только класс типа 0 или стягиваемом
(до точки) петель.
, Индикаторный частица будет двигаться по окружности угол, который зависит только от θ
. Тогда очевидно, что кумулятивный эффект перемещения одного цилиндра θ
<югу> 1, то другой θ
<югу> 2, то первое - θ
<суб> 1, а второй - θ
<югу> 2, чтобы вернуть частицу в исходное положение: нет геометрической фазы, и несмешивание все еще имеет место. Но если мы изменим настройки Heller-Тейлора и компенсировать внутренний цилиндр, мы приходим к тому, что известно как поток журнально-подшипника. О внесении эксцентриситет ɛ
между цилиндрами, этот поток имеет радиальную составляющую. В пределе ползучий потока, уравнения Навье-Стокса для потока журнально-подшипника сводятся к линейному бигармонической один, ∇ 4 ψ
= 0, для функции тока, ψ <ш>, и мы можем смоделировать эту систему с использованием аналитического решения (см [10-12] и раздел материалы и методы для получения более подробной информации). Если мы теперь выполнить цикл параметров последовательностью вращений подробно описано выше, мы приходим обратно в исходную точку, с точки зрения позиций двух цилиндров, так что, может быть, удивительно, что жидкость внутри не возвращается его начальное состояние. Проиллюстрируем наличие этой геометрической фазы на фиг.1, в котором приведен пример траектории частицы жидкости показана в виде стенки приводятся в движение через невзаимного стягиваемом петли. Поток Journal-подшипник хорошо изучен в прошлом [13-16], но никогда с стягиваемыми петель так, что этот геометрический эффект никогда не было подчеркнуто. Эта незначительная модификация протокольным в хорошо установленном потоке имеет, тем не менее, существенное влияние на динамику жидкости, как мы опишем ниже.
<Р> Заметим, что, поскольку поток производится путем взаимного цикла границ индуцирует тождественное отображение для позиции каждого элемента жидкости в последовательных циклах, проблема смешения с помощью невзаимных из них тесно связан с классом динамических систем, образованных возмущениями идентичности. Частица жидкость, которая в начале цикла находится в таком положении, достигает, в конце того же цикла, уникальной соответствующей точке ( х
', г
'), который является функция один-к-одному ( х
', г
') = G [( х
, г
)] от начальной один. Для однородных жидкостей, G также должна быть непрерывна и дифференцируема, тогда как несжимаемости следует, что G сохраняет площадь любой области точек. Другими словами, поток предполагает несжимаема гамильтонову динамику для частиц жидкости, а также отображение, что эта динамика индуцирует в одной петле область сохранения. Для стягиваемом нулевой области петли карта просто личность; каждая частица заканчивается в положении, в котором она началась. Следовательно, индуцирует цикл конечно-область, в общем, конечное отклонение от тождественного отображения и характерным значением геометрической фазы дает оценку степени этого отклонения. Так как в общем геометрической фазы возрастает с увеличением площади петли, для маленьких петель карта является малое возмущение от идентичности, тогда как петли большей площади индуцируют большие отклонения.
<Р> Рассмотрим теперь долгосрочную жидкость динамика, индуцированные повторной реализации одного и того же стягиваемом невзаимных цикл, который индуцирует данную карту. Динамика описывается многократном повторении этой карты, которая выступает в качестве стробоскопического отображения времени-периодической системы Гамильтона, состоящей из несжимаемой жидкости периодически определяется скоростью перемещения стен. Для небольших петель, отображение является малое возмущение идентичности, которую можно рассматривать как реализацию алгоритма Эйлера мнимого времени непрерывной динамической системы, определяемой этим возмущением. Таким образом, в 2D мы ожидаем, что итерации карты будут внимательно следить за траекториями этой 2D системы непрерывного интегрируемой. Таким образом, частицы жидкости будут смешиваться очень медленно в пространстве: это, так сказать, смешиваясь с "квазистатических" жидкостей. Это хорошо иллюстрируется на фиг.2 (а), где даже за квадратный контур, образованный со значениями такого размера, как θ
= П
/2 позиции частиц жидкости после последовательных циклов плавно сдвига вдоль замкнутых кривых, которые являются траектории непрерывной динамики. Траектории состоят из сегментов, которые почти следуют интегрируемые траектории 2D-потока (приближенной как карты Эйлера) до тех пор, пока не достигнет области больших фазы, где происходит хаос и гетероклинические клубки. Там частица прыгает в другой квази-интегрируемой траектории, пока он снова не достигнет области больших этапа. В типичных гамильтонова хаоса (стандартная карта, например) отображение не возмущение идентичности, а возмущение линейного сдвига (т.е. с каноническим действием угловых динамических переменных (I, φ
) после I
'= I
, φ
' = φ
+ I
') по какой причине такое поведение не как правило, рассматривается [17, 18]. Структура хаоса в этом классе динамики была значительно упускать из виду в литературе, и данное исследование открывает новый путь к пониманию этой проблемы, связанной
. <Р> В качестве геометрической фазы и соответствующего возмущения из тождества увеличение на карте, бывший аргумент начинает терпеть неудачу [19]. Более хаотический 2D-зона сохранения карты появляется и с ним соответствующие заполняющей пространство полностью хаотические траектории. Острова КАМ, как правило, становятся все меньше и меньше характерных значений геометрического роста фазы. Как мы видим на рис 2 (б) для θ
= 2 π
радиан, а тем более на фиг.2 (с) для θ
= 4 <эм> я
радиан, после 10000 циклов частица жидкости охватывает большую часть площади, доступной для него между двумя цилиндрами. Это смешивание жидкости индуцируется полностью геометрической фазы; мы можем назвать его геометрическим смешивание. Поэтому геометрическое смешивание создает хаотической адвекции [15], как это делает классический протокол журнал свиту
. <р> На рис 2 (D) -2 (е) мы покажем соответствующие распределения геометрической фазы над доменом. Значение геометрической фазы при заданном начальном положении, полученные с точки зрения конечного угла минус начальный угол в биполярных координатах (см раздел Материалы и методы для получения дополнительной информации) после одной итерации, Φ = ξ
<суб> е
- ξ
<югу> я
, наносится на цветовой шкале интенсивностей красного (положительного) и синего (отрицательный). Следует отметить, что фаза переходит в нуль на стенках, как это необходимо, но сильно варьируется в зависимости от области. В частности, для параметров θ
= 2 π
радиан (рис 2 (е)), мы видим развитие языка высоких значений геометрической фазы в некотором смысле взаимопроникающих область высоких значений фазы в противоположном смысле. Траектория показана на рис 1 показывает происхождение языка; частицы жидкости, которые адвектируется в непосредственной близости от внутреннего цилиндра первым θ
<суб> 1 шаг затем адвектируется к существенному изменению значения г
внутренним цилиндром. В результате, частица жидкости находится на совершенно другом тока от первого шага, когда внешний цилиндр начинает вращаться в обратном направлении. Как и следовало ожидать, при меньших значениях параметра этот язык отсутствует (рис 2 (d)). При еще более высоких значениях θ
, с другой стороны, (рис 2 (е)) язык обертывания дважды круглый в очень сложным образом. На фиг.2 (г) -2 (I) показано, путем построения графика эволюции линии начальных условий, как геометрическая фаза связана с динамическими структурами в потоке. Рис 2 (г), для θ
= π
/2 радиан, показывает, что, когда этот язык отсутствует, то отрезок вряд ли развивается; поток почти обратимым. Отрезки на рис 2 (ч) и 2 (i), для θ
= 2 π
и 4 π
радиан, с другой стороны, показать много растяжку, индуцированное этим языком большой геометрической фазы. Для демонстрации этого эффекта геометрической фазы на поток более подробно, на фиг.3 (В), мы наносим длину отрезка после одного цикла от угла поворота. Заметным аспектом этого участка является то, что он отображает плоскогорья разделенные периоды быстрого роста. Сравнение с рис 2 (D) -2 (е) показывает, что проникновение языка больших значений геометрической фазы через этот участок линии, индуцирующего растяжения. Язык проникает в первый раз перед θ
= 2 π
, а затем второй раз перед θ
= 4 π
, поэтому производить два прыжки; между этими скачками эволюция сегмента линии значительно медленнее. Для данной стоимости энергии, которая масштабируется с общим смещением без знака стен, геометрическая смешивание поэтому является более эффективным для большого значения θ
.
<Р> Поток журнально-подшипник только один член класса потоков, которые отображают геометрическое смешивание. В открытых потоках, один есть экземпляры, такие как хорошо известный Purcell пловец, который можно рассматривать как деятельность через геометрической фазы. Другой замкнутый поток, который был изучен на ранней стадии в хаотической адвекции является прямоугольным поток полость, в которой одна или более стенок заполненных жидкостью прямоугольный контейнер может перемещаться, их в виде конвейерных лент [15, 20]. Как и в случае первых исследований журнала подшипнике, эти смесительные протоколы подразумевают кумулятивный относительное смещение стенок контейнера. Тем не менее, так же, как и в случае журнал водоносного можно ввести геометрическую фазу, возвращая все стены в их исходные относительные положения после того, как петли в параметрах. В более общем смысле, можно представить себе потоков, индуцируемых контейнера, в котором стены не движутся как твердые тела, но вместо этого может деформироваться в продольном направлении и /или по касательной вдоль невзаимного цикла, чтобы произвести эффективное перемешивание. Например, можно было бы рассмотреть случай эластичного мешка, содержащего жидкость и подвергается действию периодической последовательности сдавливание-расправления вокруг одной из его секций с компенсирующим расправления-выдавливание действия вокруг другого. Этот цикл будет явно вызывать поток возвратно-поступательные непригодной для эффективного смешивания, но опять геометрическая фаза может быть сделано, чтобы существовать, если эта пространственно стационарной конфигурации были заменены одним, распространяющейся вдоль оси мешка.
перистальтические смешивания
<р> желудок представляет собой биологический пример такого потока полости [21, 22]. Человеческий желудок сильный мышечный сосуд между пищеводом и тонкой кишки. Это не просто камера для хранения пищевых продуктов, но и смеситель, где готовят химуса. Человеческий желудок имеет объем L
3 около 330 мл, в то время как вязкость μ
из химуса порядка 1 Па · с, его плотность ρ
≈ 10 3 кг м -3, а максимальный поток скорости V
наблюдается в диапазоне 2,5-7,5 мм s -1 [21]. Из этих данных можно оценить число Рейнольдса Re
= ρVL
/ μ
лежать в диапазоне 0,2-0,5. Таким образом, мы можем заключить, что в желудке инерции жидкости человека имеет лишь ограниченное значение, и в любом меньшем животное будет незначителен. Отметим, что предыдущая работа на желудочную перемешивания в основном рассматривался случай инерционных вкладов [21, 23, 24], для которых динамические ограничения, обсуждаемые здесь, не применяются.
<Р> Смешение желудка вызвано перистальтического waves- поперечных бегущих волн сжатия-которые распространяются вдоль стенок желудка у некоторых 2,5 мм s -1. Они инициируются примерно каждые 20 секунд, и принять около 60 сек, чтобы передать длину желудка, поэтому 2-3 волны присутствуют в одно время, в то время как в среднем ширина живота, как волна проходит в 0,6 раз по сравнению с нормальной шириной [21 , 22]. Таким образом, мы имеем их скорость с
= 2,5 мм s -1, частота ω
= 0,05 Гц, а оттуда длина волны λ
= с <бр /> со
= 5 см, а их амплитуда B
= 1/2 × 0,6 L
≈ 2 см. Эти волны заставляют желудок через невзаимного петли в пространстве формы, в результате которого, как ожидается геометрического смешивания. Можно дать грубую оценку размера ожидаемой геометрической фазы, воспользовавшись результатами, полученными для другой геометрической задачи фазы: что из низкого числа Рейнольдса микроорганизмов плавание. Многие бактерии плавать деформируя их тела таким же образом, как и перистальтической волны желудка и их скорость была хорошо оценена путем моделирования таких деформаций, как плоских волн [25]. Аналогичные расчеты для желудка оказывают скорость потока, вызванное перистальтических волн V
=
П С ( б
/ λ
) 2 , который выходит примерно 1 мм s -1, откуда водоизмещение около 6 см в перистальтический цикл, как ожидается, или, принимая во внимание круговой желудок радиуса L, геометрической фазы порядка 2 радиан.
согласно г
<югу> ш
( х
, т
) = 1+ б
грех ( кх
- ωt
) в ( х
, г
) система координата. Поток внутри полости получается путем интегрирования уравнений Стокса для поля скоростей ( и
, v
) с соответствующими граничными условиями для перистальтической волны на верхней границе, у
= 0 и v
= ∂ г
<югу> ж
/∂ т
в г
= г
<югу> ш
( х
, т
), и симметрии граничные условия на г
= 0 . Боковые стенки деформируются по вертикали, чтобы соответствовать вертикальной скорости перистальтической волны в х
= 0 и х
= 2 π
. На рисунке 4 (а) черные сплошные линии представляют собой линии тока, индуцированного движения жидкости в полости из-за волны перистальтики. Контурный график соответствует усредненной по времени скорости в течение одного полного цикла перистальтического. Области максимальной средней скорости близки к оси симметрии, в то время как у стены средняя скорость равна нулю и не производится не среднее движение.
<Р> Рассмотрим смешение пассивного скаляра которого начальное пространственное распределение в т
= 0 задается размытый стадии (как представлено в контурной карте рис 4 (б). временная эволюция этой пространственной концентрации получается интегрирования уравнения адвекции-диффузии для характерного числа Пекле, Пе
= cλ
/ D
<суб> кашица
представитель процесса смешивания в желудке. Как характерный коэффициент диффузии химуса является, в лучшем случае, порядка молекулярной диффузии крупных макромолекул D
<суб> кашица
≤ 10 -6 см
2 / s
, Пе
»1 и адвективные вклады доминировать в процессе перемешивания. Рисунок 4 (с) представляет собой пространственную концентрацию пассивного скаляра χ
после 20 циклов перистальтики (то есть после того, как перемасштабирована время T
= т
/ T
* = 20, где T *
представляет период цикла) для Пе
= 15 × 10 3. Поток, индуцированный перистальтики накапливает конечную геометрическую фазу после каждого цикла жидкость элементы растягиваются и сложенным и, как следствие, образуются тонкие нити, которые облегчения смешивания внутри полости.
<Р> Получаем ГФ путем интегрирования траектория пассивной примеси в течение одного полного цикла, с равномерно распределенными начальными условиями в области [0, 2 π
] × [0, г
<югу> со <бр> ( х
, 0)]. Евклидово расстояние между начальной и конечной позиции после одного цикла дает оценку геометрической фазы. Контуры на фиг.4 (г) представляют геометрической фазы системы. Можно видеть, что максимальные смещения наблюдаются в центральной области полости, где создаются нити. Следует отметить, что участки на рис 4 (г) с небольшими смещениями соответствуют областям, которые остаются несмешанные на фиг.4 (с). Таким образом, и, несмотря на равномерном радиуса полости в нашей минимальной геометрической модели, смешивание не пространственно однородной. Регионы в центральной части полости образуют тонкие нити, которые усилить смешивание, в то время как области, близкие к боковым и на верхние стенки остаются практически несмешанные после 20 циклов. Даже дальнейшие неоднородности, как ожидается, для более точных геометрий, с изменением среднего диаметра стенки [27], конкретные сроки открытия и закрытия привратника с перистальтики [28] и взаимодействий между фундальном /сердечной области желудка [29], все из которых, как известно, особенность для смешивания внутри желудка [30].
<р> Желудочные схваток, которые соответствуют стоячей волны сродни нулевой зоне взаимного контура. Как мы ожидали, для случая, журнально-подшипникового, взаимные петли вызывают поток, который не генерирует никакого смешивания. Это показано на фиг.5 (б), где поле концентрации после 20 циклов границ деформирующих как стоячей волны изображен. Так как наведенный геометрическая фаза равна нулю, смешивание контролируется только (медленной) диффузии.
<Р> Важность геометрического смешивания в желудке, могут быть оценены ссылкой на случаи, в которых оно нарушается. Желудок, как сердце, с электрической активностью из области кардиостимулятора, стимулирующего колебания; в этом случае быть бегущими волнами перистальтики. Если эта система не работает надлежащим образом, может быть парез желудка или фибрилляция [31, 32], в которой перистальтические волны становятся неупорядоченной. Мы сформировали такие беспорядочные деформации перемежая перистальтические волны, распространение скорости C
выбираются случайным образом из равномерного распределения нулевого среднего значения. Скалярное поле <ЕМ> χ
остается почти несмешанные по сравнению с перистальтической случае после эквивалентного времени интегрирования с перемешиванием в основном под контролем снова путем медленной диффузии (рис 5 (с)). Таким образом, в наших терминах, есть плохое смешивание или нет смешивания в гастропарезу, потому что не петля вокруг пространства форм, так что не средняя геометрическая фаза, и вместо того, чтобы случайные перистальтические волны вызывают только смешивание и несмешивание.
<Р> для того, чтобы сравнить степень перемешивания в трех случаях, рассмотренных в настоящем документе (перистальтика (PW), стационарные (ЕО) и случайные (RW) волны), вычислим для каждого цикла дисперсии пространственного поля концентрации [33, 34], σ
= <( χ
- < χ
>) 2> 1/2, где <> обозначает пространственное среднее. Фиг.5 (а) представляет собой эволюцию σ
с числом циклов. Это свидетельствует о более высокой эффективности перемешивания реализованный в перистальтики геометрического смешивания.
Обсуждение
&л; 1.
<р> Поток журнально-подшипник широко используется для изучения процесса перемешивания в ламинарных потоков. На фиг.6 показана схема конфигурации исследуемой в настоящей заявке. Наружный цилиндр радиуса <ет> R
<суб> из
вращается с угловой скоростью <югу> из
, в то время как внутренний цилиндр радиуса <ет> R
<суб> в
вращается с угловой скоростью <югу> в
. Эксцентриситет внутреннего цилиндра задается ɛ
. В пределе, когда вязкие силы пренебрежимо малы, в результате поток получается путем интегрирования бигармонического уравнения для функции тока ∇ 4 ψ
= 0 с соответствующими граничными условиями на стенках цилиндров.
<югу> вне
это решение для функции тока потока, вызванного внешним цилиндром, в то время как ψ
<югу> в
соответствует решению функции тока потока, вызванного внутренним цилиндром. Угол покрывается цилиндром в течение одного цикла зависит от его угловой скорости по формуле (2), где субиндекс я
обозначает внешнюю или внутренний цилиндр и T *
представляет период цикла , Так, при моделировании рассматриваемых в данной работе угловая скорость цилиндра постоянна, Θ <югу> я
= T
* Ω <югу> я
. Этот поток допускает точное решение [11] для функции тока, когда проблема записывается в биполярных координатах, ( ξ
, η
). Декартовы координаты ( х
, г
) могут быть восстановлены в соответствии с (3), где (4) Следуя [11] решение для внутренних и внешних функций потока дается формулой (5 ) где H
= б
/( с
2 + s
2) 1/2, с s
= зт £,
греху η
и с
= cosξ
соз η
- 1. Кроме того, (6) (7) и (8) (9) withwhere ξ
<суб> в
и ξ
<югу> из
представляют поверхности внутреннего и наружного цилиндров, соответственно, и Δ,, Δ *, ч
<югу> 1, ч
<суб> 2, ..., ч
<суб> 8 задаются
<р> После того, как поток оценивается, были получены траектории частиц интегрирования (10) (11) интегрирование уравнений (10) и (11) было осуществляется с четвертого порядка схеме Рунге-Кутта. После того, как один полный цикл, оба цилиндра заканчиваются в исходное положение, в то время как частицы отступая от исходного положения ( ξ
<суб> I
, η
<суб> я
) расположены в ( ξ
<югу> F
, η
<югу> е
).
Микробиом кишечника и ВЗК - связь, возможно, в диете, говорится в исследовании
Ученые разрабатывают пептиды, которые восстанавливают баланс кишечных бактерий и предотвращают атеросклероз.
Что делать с гепатитом С?
Микробиом спермы выявлен с помощью секвенирования РНК
Недавно обнаруженные крупные фаги стирают границу между жизнью и неживой
Микробиом человека сокращает гликаны слизистых оболочек,
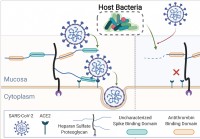
Белок SARS-CoV N вызывает выработку IFN-β, провоцируя убиквитинирование RIG-I,
находит исследование Многие представители семейства Coronaviridae, такие как ближневосточный респираторный синдром (MERS), тяжелый острый респираторный синдром (ОРВИ), и тяжелый острый респираторный с
Тяжелые осложнения COVID-19, связанные с нарушением кишечного барьера
Основное внимание в исследованиях нынешней пандемии коронавирусного заболевания 2019 (COVID-19) было направлено на необходимость понимания действующих механизмов, вызывающих различные проявления и осл
Мало доказательств наличия тромбоцитопении, связанной с мРНК COVID-19,
предлагает новое исследование FDA Несмотря на то, что для противодействия пандемии коронавирусной болезни 2019 г. (COVID-19) было выпущено множество вакцин, Сообщалось о некоторых серьезных побочных э