Keverés folyadék a tartályban alacsony Reynolds számozással egy inertialess környezettel nem triviális feladat. Dugattyús mozgások csupán vezet ciklus keverés és szétválasztás, így folyamatos forgás, amint használják számos technológiai alkalmazásokat, úgy tűnik, hogy szükséges. Azonban van egy másik megoldás: mozgása a falak egy ciklikus módon, hogy bemutassuk egy geometriai fázist. Megmutatjuk a folyóirat-csapágy flow, mint egy modell, amely geometriai keveredés egy általános eszköz segítségével alakítható határok visszatérni ugyanabba a helyzetbe keverni folyadék alacsony Reynolds-szám. Ezután szimulálni egy biológiai példa: megmutatjuk, hogy a keverés a gyomorban funkciókat, mert a "hasa fázisban" perisztaltikus mozgása a falak egy ciklikus módon bevezeti a geometriai fázis, amely elkerüli szétválasztás. Katalógusa
Citation: Arrieta J Cartwright JHE, Gouillart E, Piro N, O Piro, Tuval I (2015) Geometriai keverés, perisztaltika, és a geometriai fázis a gyomor. PLoS ONE 10 (7): e0130735. doi: 10,1371 /journal.pone.0130735 katalógusa
Szerkesztő: Christof Markus Aegerter, University of Zürich, Svájc katalógusa
Beérkezett: március 30, 2013; Elfogadva: 23. május 2015; Megjelent: július 8, 2015 katalógusa
Copyright: © 2015 Arrieta et al. Ez egy nyílt hozzáférésű cikk feltételei szerint terjeszthető a Creative Commons Nevezd meg! Licenc, amely engedélyezi a korlátlan használatát, a forgalmazás és a reprodukció bármilyen adathordozón, feltéve, hogy az eredeti szerző és a forrás jóváírásra katalógusa
Forrás: A szerzők elismerik a pénzügyi támogatást a támogatás FIS2010-22322-C02-01 /02-re a Tudományos és innovációs (MICINN) és a "subprograma Ramon y Cajal" (IT). A finanszírozók nem volt szerepe a tanulmány tervezés, adatgyűjtés és elemzés, döntés, hogy közzéteszi, vagy a készítmény a kézirat. Katalógusa
Érdekütközés: A szerzők kijelentették, hogy nem ellentétes érdekek léteznek. Katalógusa
Bevezető
Hogyan lehet folyadékot kell keverni alacsony Reynolds-szám? Az ilyen keverés általában végre, keverővel, egy forgó eszköz a tartályon belül, amely létrehoz egy komplex, kaotikus áramlását. Alternatív megoldásként hiányában, keverővel, a tartály forgását, falak maguk tud végezni a keverés, mint ahogyan betonkeverőben. Alkalmanként azonban keverés megkísérelt egy ciklikus deformáció a tartály falai, amely nem teszi lehetővé a nettó relatív elmozdulását a megfelelő felületek, helyzeteket, amelyek gyakran fordulnak elő mind a mesterséges eszközök és az élő szervezetekben. A legalacsonyabb Reynolds-számok mellett, amit az úgynevezett kúszó áramlási feltételek, folyadék tehetetlenség elhanyagolható, folyadékáramlás reverzibilis, és az inverzió a mozgás a keverő vagy a falak vezet-ig zavarok miatt részecske diffúzió-to szétkeverés, Taylor [1] és Heller [2] bizonyították. Ez úgy tűnik, hogy zárja a alternáló mozgást keverjük folyadék alacsony Reynolds-számok; úgy tűnik, hogy vezet örökös ciklusok a keverés és szétkeverés. Felmerül tehát a kérdés, hogy hogyan ciklikus változások az alakja a konténerek vezethet hatékony keverés. Tekintsünk egy biológiai esetén üreg flow: a gyomrot. A gyomorban étel és az ital kevert homogén folyadék nevezett gyomorpép, amelyet azután emésztett a belekben. A gyomor keverő által termelt ún perisztaltika: a gyomor falai mozgó ritmikus módon. Matematikai megfogalmazásban, a forma a gyomor falai megy zárt ciklusban a tér formák során minden perisztaltika ciklusban. Nyilvánvalóan csak formálni ciklusok, amelyek nem igényelnek kumulatív nettó elmozdulás bármely két szakaszok a gyomor lehet tekinteni. Hogy akkor ez a perisztaltikus mozgás a gyomor falak képes előállítani keverés, különösen olyan állatok, amelyekben a gyomor méretei olyanok, hogy a folyadék tehetetlensége a gyomor tartalma elhanyagolható?
A megoldás erre a találós magában foglalja a koncepció geometriai fázis katalógusa. A geometriai fázis [3] egy példa anholonomy: a hiba a rendszer változó, hogy visszatérjen az eredeti értékükre után egy zárt kör a paramétereket. Ebben a levélben azt javasoljuk azt, amit mi geometriai keverés: a használata a geometriai fázis bevezetett nonreciprocal kerékpáros a deformálható határainak tartály, mint egy eszköz lyadékkeverő alacsony Reynolds-szám. Például annak, hogy ez a folyamat vezet a hatékony keverés, használjuk a jól ismert kétdimenziós mixer alapuló folyóirat csapágy áramlását, hanem olyan sokat kevésbé tanulmányozott forgatás protokoll, amely megfelel a geometriai kényszerek ciklikus határ deformációk. Mi végül azt mutatják, hogy a bélmozgást, amellett hogy hozzájárul a fontos biológiai funkciókat, mint a folyadék fuvarozás az egyes csöves szervek [4, 5], vagy jelző egész komplex biológiai struktúrák [6], teljesíti központi szerepét a gyomor keverő és az emésztés [7-9] működtetésével köszönhetően geometriai fázis a gyomorban. katalógusa Eredmények katalógusa Journal csapágy flow katalógusa Taylor [1] és Heller [2] használta Couette áramlása összenyomhatatlan folyadék tartalmazott két koncentrikus hengerből bizonyítani folyadék szétválasztás idő miatt visszafordíthatóságára Stokes rendszer. Ezek azt mutatták, hogy miután forgó hengerek keresztül egy bizonyos szögben, lehetséges, hogy érkezik vissza a kezdeti állapot-to unmix az áramlási megfordításával ez forgás révén azonos szögben az ellenkező megjelölés, még ha ez a szög elég nagy ahhoz, hogy a blob festék kerül a folyadék már látszólag jól összekeverjük. Figyelembe véve a paraméterei a készülék a pozíciókat a külső és belső hengeres tartály falai megadott sorrendben a szögek θ katalógusa 1 és θ katalógusa 2 egy adott kiindulási pont, a geometriai fázis merülhetnek fel a vezetés ez a rendszer köré egy hurkot a paraméter térben. katalógusa a folyadék rendszer a Stokes rendszer, mint a miénk, mint a tehetetlenség elhanyagolható a mozgás, definíció mindig adiabatikus és csak által indukált változás a paraméterek: a pozíciókat a henger. Ezért az ebből eredő fázis után egy teljes ciklus paraméterek geometriai fázis. A Heller-Taylor bemutató paraméter hurok nagyon egyszerű: θ katalógusa 1 első növekszik egy bizonyos összeget, majd csökken az azonos mennyiségű, míg θ katalógusa 2 rögzítve marad. Ez a hurok körülveszi nincs terület, és visszafordíthatósága biztosítja, hogy a fázis nulla. Bonyolultabb zéró terület katalógusa hurkokat lehet kialakítani kombinálásával egymás tetszőleges pár kölcsönös forgatások mindkét henger, és ők is vezetnek null fázis. Nevezzük ezeket a konstrukciókat kölcsönös ciklus Minden zéró terület kölcsönös hurkokat összehúzódásra, de van még sok más körülzáró véges területen. Ahhoz, hogy egy véges területen nem kölcsönös összehúzódó hurok tudjuk például, forgatás első henger, akkor a másik, majd fordított az első, és végül fordított a másik. Azonban a koncentrikus hengerből az áramvonalak koncentrikus körök; ha haladunk az egyik henger szöggel θ katalógusa, a nyomjelző részecske mozog egy kör mentén egy szöget, hogy csak attól függ, hogy θ katalógusa. Akkor nyilvánvaló, hogy a kumulatív hatása mozgó egyik henger θ katalógusa 1, akkor a másik θ katalógusa 2, akkor az első - θ katalógusa 1, és a második - θ katalógusa 2, az, hogy visszatérjen a részecske eredeti helyzetébe: nincs geometriai fázis, és szétválasztás még mindig fennáll. De ha módosítja a Heller-Taylor telepítést és ellensúlyozza a belső henger, eljutunk az úgynevezett folyóirat-csapágy áramlását. Bevezetéséről szóló excentricitás ɛ katalógusa hengerek közötti, ez az áramlás a sugárirányú komponense. A kúszás-fogyasztási határérték, a Navier-Stokes egyenletek a folyóirat-csapágy áramlás csökkenti a lineáris biharmonic egy, ∇ 4 ψ katalógusa = 0, az adatfolyam funkciót, ψ Megjegyezzük, hogy mivel az áramlási által kölcsönös ciklus határai indukál identitás térkép a pozíciókat az egyes folyékony elem egymást követő ciklusokban, a probléma a keverés által nonreciprocal is szorosan kapcsolódik az osztály a dinamikus rendszerek által alkotott perturbációira a személyazonosságát. Egy folyadék részecske, hogy az elején a hurok abban a helyzetben van, eléri, a végén az azonos hurok, egy egyedülálló megfelelő pont ( X Nézzük a hosszú távú folyadék dinamika által kiváltott ismételt megvalósulását mutatja összehúzódó nem kölcsönös hurok, amely indukálja az adott térképet. A dinamika által leírt ismételt iterációs ez a térkép úgy működik, mint a stroboszkóp-térkép az idő periodikus Hamilton rendszer által alkotott folyadékok áramlásának időközönként hajtja a mozgás a falakon. A kis hurok, a térkép egy kis zavarása az identitás lehet elképzelni, mint a végrehajtás az Euler algoritmus egy feltételezett folytonos dinamikai rendszer által meghatározott ezen perturbáció. Ezért arra számítunk, hogy a 2D ismétléseken a térkép szorosan nyomon fogja követni a pályáját a 2D-s folyamatos rendszer, amely integrálható. Ezért a folyadék részecskék keverjük nagyon lassan az űrben: ez, hogy úgy mondjam, a keverés a "kvázi-statikus" folyadékok. Ez szépen szemlélteti a 2. ábra (a), ahol még egy négyzet alakú hurok képződött értékekkel akkora, mint θ katalógusa = π katalógusa /2 pozícióinak folyékony részecskék után egymást hurkok simán műszak mentén zárt görbék, amelyek a pályáját folyamatos dinamikáját. A pályák szegmenseiből állnak, hogy közel kövesse a integrálható pályái 2d flow (közelíteni, mint egy Euler térkép), amíg el nem éri a régió nagy fázis, ahol a káosz és heteroclinic gubanc fordul elő. Ott a részecske beugrik egy másik kvázi-integrálható röppálya, amíg újra el nem éri a régióban nagy szakasza. Tipikus Hamilton káosz (a normál térkép, például) a térkép nem a zavarása az identitás, hanem egy zavarása lineáris nyírási (azaz a kanonikus akció látószögű dinamikai változók (I, φ katalógusa) következő I Mivel a geometriai fázis és a megfelelő perturbáció a személyazonosság térkép növekedése, a korábbi érvelés kezd nem [19]. A kaotikus 2D-terület leképezés kiderül, és vele a megfelelő térkitöltő teljesen kaotikus pályákra. A KAM szigetek jellemzően egyre kisebb és kisebb, mint a jellemző értékek geometriai fázis növekedése. Amint látjuk a 2. ábra (b) θ katalógusa = 2 π katalógusa radiánmérték és még inkább a 2. ábra (c) θ katalógusa = 4 π radián katalógusa, miután 10000 ciklus a folyadék részecskék fedezte a legtöbb területen rendelkezésére álló két henger. Ez lyadékkeverő indukált teljesen a geometriai fázis; nevezhetjük geometrikus keverés. Geometriai keverés teremtenek kaotikus advekciós [15], akárcsak a klasszikus folyóirat-csapágy protokoll. Katalógusa A 2. ábrán (d) 2 (f) azt mutatják, a megfelelő eloszlás geometriai fázist a domain. Az érték a geometriai fázis egy adott kiindulási helyzetben, kapott tekintve a végső szög mínusz a kezdeti szöget a bipoláris koordinátákkal (lásd az Anyagok és módszerek fejezetben a további részleteket), miután egy iteráció, Φ = ξ katalógusa f katalógusa - ξ katalógusa i A folyóirat-csapágy áramlás egyike osztályának tagja áramlások megjelenő geometriai keverés. A nyílt-flow, az egyik esetben, mint például a jól ismert Purcell úszók, hogy lehet tekinteni, mint keresztül működik egy geometriai fázisban. Egy másik zárt áramlási hogy vizsgáltuk korai szakaszában a kaotikus advekciós van a négyszögletes üreg áramlás, amelyben egy vagy több, a falak egy folyadékkal töltött négyszögletes tartály lehet mozgatni, létesül szállítószalagok [15, 20]. Mint abban az esetben a korábbi tanulmányok a folyóirat-csapágy, ezek keverés protokollok jelenti a kumulatív relatív elmozdulás a tartály falait. Azonban ugyanúgy, mint a Journal-csapágy esetében lehet bevezetni egy geometriai fázis visszaküldésével összes falain át a kezdeti relatív pozíciók után egy hurok a paramétereket. Általánosabban, lehet elképzelni az áramlások által indukált egy tartályt, amelyben a falak nem mozognak, mint merev testek, de ahelyett, deformálódhat hosszirányban és /vagy érintőirányban mentén nonreciprocal ciklus előállítása érdekében a hatékony keverést. Például, mérlegelhető az esetben, ha egy rugalmas zsák, amely a folyadék és az akció időszakos préselés-puffadás körüli szekvencia egyik szakaszok kompenzáló puffadás-szorította akció másik körül. Ez a ciklus egyértelműen indukál váltakozó áramlási alkalmatlan a hatékony keverés, de megint egy geometriai fázis lehetne tenni, hogy létezik, ha ez a térben álló konfigurációt váltották egy irányba terjednek a zsák tengely. Katalógusa Perisztaltikus keverés katalógusa A gyomor egy biológiai például egy ilyen üreg áramlás [21, 22]. Az emberi gyomor egy erős izmos befogadóedény között a nyelőcső és a vékonybélben. Ez nem csak egy tároló kamrát az élelmiszer, hanem egy keverőben, ahol a béltartalom állítjuk elő. Az emberi gyomor térfogata L katalógusa 3 330 ml, míg a viszkozitás μ Vélemények a béltartalom van a rend 1 Pa s, sűrűsége ρ A gyomor keverő által előidézett perisztaltikus waves- keresztirányú utazó hullámok összehúzódás-felszaporodó mentén a gyomor falai a 2,5 mm-s -1. Ők kezdeményezték körülbelül minden 20 s, és némi 60 s átadni a hossza a gyomor, így 2-3 hullámok vannak jelen egy időben, míg átlagosan a gyomor szélességű, mint a hullám halad az 0,6-szerese a normál szélességű [21 , 22]. Mi tehát a sebesség c katalógusa = 2,5 mm s -1, frekvencia ω katalógusa = 0.05 Hz és onnan hullámhossz λ katalógusa = c hatását mutatják ebben a fázisban már épített egy minimális modell a gyomor alatt perisztaltika, mint rajzolt ábra 4 (a), és tovább részletezi az anyagok és módszerek fejezetben. Mi már szándékosan csökkentette a geometriai, dinamikai és funkcionális összetettsége a gyomor és a modell 2D részén egy cső alakú gyomor egységes sugár, valamint a zárt pylorus és a nyelőcső szelepek, hogy összpontosítson a szerepe perisztaltikus összehúzódások játszhat keverés belül zárt inertialess üreg. Hasonlóképpen, az általunk kezelt a gyomorpép, mint egy newtoni folyadék, így a komplex összekapcsolása viszkoelaszticitás jövőbeli munka, mivel a léte vagy nem a geometriai keveredés a gyomorban független a viszkoelasztikus tulajdonságait a béltartalom. Hasonló modellt alkalmaztunk [4, 26], hogy értékelje szállítás perisztaltikus szivattyúzás végtelen karcsú csövekbe. Ebben a modellben a perisztaltikus hullám deformálja a felső és alsó határát szimmetrikus üregének képarány π katalógusa szerint z katalógusa w katalógusa ( x katalógusa, t katalógusa) = 1 + b katalógusa sin ( kx katalógusa - ωt katalógusa) a ( x katalógusa z katalógusa) -coordinate rendszer. Az áramlási belül az üreget integrálásával kaptunk Stokes egyenletek sebességterének ( u Úgy véljük, a keverés a passzív skalár amelynek kezdeti térbeli eloszlása a t katalógusa = 0 adja a homályos lépés (képviselt a kontúr térképét 4. ábra (b). az időbeli alakulását az a térbeli koncentráció kapjuk integráló advekciós-diffúziós egyenlet karakterisztikus Péclet szám Pe katalógusa = CX katalógusa / D katalógusa béltartalom katalógusa képviselője a keverési folyamat a gyomorban. Mivel a jellemző diffúziós a béltartalom van, legfeljebb a sorrendben a molekuláris diffúzió nagy makromolekulák D katalógusa béltartalom katalógusa ≤ 10 -6 cm katalógusa 2 / s katalógusa, Pe megkapjuk a geometriai fázis integrálásával a pálya a passzív skalárokkal több mint egy teljes ciklust, egyenletesen elosztva a kezdeti feltételeket a tartomány [0, 2 π katalógusa] × [0, z katalógusa w gyomor összehúzódások, amelyek megfelelnek egy állóhullám rokonságban vannak egy nulla terület kölcsönös hurok. Ahogy várható a folyóirat-csapágy esetben kölcsönös hurkok indukálnak áramlás, amely nem generál keverést. Ez látható az ábrán az 5 (b) ha a koncentráció mező után 20 ciklus a határok deformáló, mint egy állóhullám van ábrázolva. Mivel az indukált geometriai fázis nulla, a keverést csak vezérli (lassú) diffúzió. Katalógusa A fontos geometriai keveredés a gyomorban is értékelik hivatkozva azt is, amikor megbomlik. A gyomor, mint a szív, az elektromos aktivitás pacemakertől régió stimuláló rezgések; ebben az esetben pedig utazó hullámok perisztaltika. Ha ez a rendszer nem működik megfelelően, nem lehet gastroparesist vagy gyomor fibrilláció [31, 32], amelyben a perisztaltikus hullámok rendezetlen lesz. Hoztunk létre, mint a rendezetlen deformációk által vegyítve perisztaltikus hullámok terjedési sebessége, amelynek c katalógusa véletlenszerűen kiválasztott egy egyenletes eloszlását nulla várható. Skalármező χ katalógusa pedig szinte nem kevert képest perisztaltikus ügy után egyenértékű integrálási időt, a keverést, többnyire irányított ismét lassú diffúzió (5. ábra (c) pont). Így a mi fogalmaink szerint, van rossz keverési vagy nincs keveredés gastroparesist mert nincs egy hurkot a tér formák, így nem átlagos geometriai fázis, és helyette véletlenszerű perisztaltikus hullámok indukálnak csak a keverés és a szétválasztás. Katalógusa összehasonlítani a mértéke keverés a három vizsgált esetben a leírásban (perisztaltika (pw), helyhez kötött (sw) és a véletlen (rw) hullámok), kiszámítjuk az egyes ciklusok varianciája a területi koncentráció terén [33, 34], σ katalógusa = <( χ katalógusa - < χ katalógusa>) 2> 1/2, ahol a <> jelöli a térbeli átlagos. 5. ábra (a) amely az evolúció σ katalógusa a ciklusok számát. Ebből kiderül, a magasabb keverési hatékonyságot realizált perisztaltika geometrikus keverés. Katalógusa Vita katalógusa Összefoglalva, már bevezette a geometriai keverő, amely keverés következtében felmerülő mértani fázis által kiváltott egy összehúzódásra nem kölcsönös ciklus meghatározó paraméterek az alak a tartályba. Kiderült, hogy a keverés hatékonysága megbecsülhető a nyújtás anyag vonalak nagyjából arányos a geometriai fázis. Keverés a megfelelő áramlások is tekinthető, mint az eredmény a káosz keletkezett a leképezés mozgását leíró folyadék elemek egy ciklus alatt. Amikor a ciklus kölcsönös, ez a térkép a személyazonosító és egy kis eltérés a kölcsönösség megfelel egy kis eltérés a személyazonosság térképet. A kaotikus tulajdonságai térképek szomszédos azonosságát is alig tanulmányozták a múltban. Azt is felmerülhet egészen más összefüggésben numerikus integrálási módszerek közönséges differenciálegyenletek a határt, ahol a lépés nagysága nullához. [19] Eredményeink tehát szintén relevánsak a jellemzésére káosz ebben az osztályban a rendszer. Végül pedig azt mutatják, hogy egy ilyen geometriai fázis a "hasa fázis" [35] -May található a gyomor állatok ahol Re katalógusa < 1. katalógusa alátámasztó információk katalógusa Journal csapágy flow katalógusa A folyóirat-csapágy áramlás már széles körben alkalmazott, hogy tanulmányozza a folyamat keverés lamináris áramlás. 6. ábra egy vázlatot a konfigurációs vizsgált leírásban. A külső henger sugara R katalógusa ki katalógusa forog szögsebességgel Ω ki katalógusa, míg a belső henger sugara R mivel a linearitás a probléma a megoldás az adatfolyam funkciót felírható (1), ahol ψ katalógusa ki katalógusa a megoldás a patak funkció az áramlás által indukált külső henger, míg a ψ Ha az áramlás értékeljük, a pályák a részecskék kaptuk integráló (10) (11) az integráció a egyenletek (10) és (11) volt elvégezni a negyedrendű Runge-Kutta rendszer. Miután egy teljes ciklus, mindkét henger befejeződhet az eredeti helyzetükbe, miközben a részecskék onnan kiinduló álláspontját ( ξ katalógusa i
. Annak érdekében, hogy megvizsgálja kevésbé triviális hurkot, akkor először vegye figyelembe, hogy a paraméter tér homotóp a 2-tórusz. Hurkot egy ilyen helyet lehet osztályozni, hogy hány teljes kiderül, hogy a két paraméter felhalmozódnak mentén a hurok. Vegyük észre azt is, hogy a viszonylagos elfordulását 2 π
a falak között hozza a tartály az eredeti konfiguráció, kivéve egy globális forgatást. Mivel mi érdekli alakú hurkok lehet elérni anélkül, hogy a halmozott nettó elmozdulás a felületek a konténerek, meg kell vizsgálni csak az osztály-es típusú 0 vagy összehúzódásra katalógusa (egy bizonyos pontig) hurkok.
, és mi is modellezni ezt a rendszert felhasználva az analitikus megoldás (lásd [10-12] és az anyagok és módszerek fejezetben további részleteket). Ha most végre egy paraméter hurok sorozata által forgatások fent részletezett érkezünk vissza a kiindulási pontot a szempontból az álláspontok a két henger, ez így van, talán meglepő, hogy a folyadék belsejében nem tér vissza az eredeti állapotába. Mi szemléltetik a jelenléte ezt a geometriai fázis az 1. ábrán, ahol egy példa a pálya egy folyadék részecske látható, mint a falak vannak meghajtva keresztül nonreciprocal összehúzódni hurok. Journal-csapágy áramlás már sokat vizsgálták a múltban [13-16], de soha nem összehúzódó hurkok úgy, hogy ez a geometriai értelemben sohasem hangsúlyozták. Ez kisebb protocolary módosítást egy jól megalapozott folyamnak, mindazonáltal jelentős hatása van a folyadék-dinamika, ahogy leírják alább. Katalógusa
', Z
'), amely egy-egy funkciót ( x katalógusa " z katalógusa) = G [( x katalógusa, z katalógusa)] a kezdeti egy. A homogén folyadékok, a G is kell lennie folyamatos és differenciálható, mivel összenyomhatatlan azt jelenti, hogy a G megőrzi a terület minden domén pontot. Más szóval, összenyomhatatlan áramlási azt jelenti, Hamilton dinamikáját a folyadék részecskék, és a térkép, hogy ez a dinamika indukál egy hurok terület megőrzése. Mert összehúzódásra zéró terület hurkok térképen egyszerűen az identitás; minden egyes részecske végződik abban a helyzetben, amelyben elindult. Ezért, egy véges-terület hurok indukálja, általában egy véges eltérés a személyazonosság térkép és egy jellemző értéke a geometriai fázis becslést ad a mértékét az eltérés. Mivel általánosságban a geometriai fázis növekszik a terület a hurok, a kis hurkot a térképen egy kis perturbáció távol a személyazonosságát, míg hurkok nagyobb területen okozott nagyobb eltérésekkel. Katalógusa
'= I
, φ katalógusa' = φ katalógusa + I
) ami miatt ez a viselkedés nem normál esetben [17, 18]. A szerkezet a káosz ebben az osztályban a dinamika már jelentősen figyelmen kívül a szakirodalomban, és a jelen kutatás megnyit egy új Avenue megértéséhez ennek társult problémát.
ábrázoltuk a színskála intenzitást piros (pozitív) és a kék (negatív). Megjegyezzük, hogy a fázis megy nullára a falakon, ahogy kell, de változik erősen az egész tartományban. Különösen paraméterei θ katalógusa = 2 π radián katalógusa (2. ábra (e)), látjuk a fejlődés egy nyelv magas értékek a geometriai fázis értelemben hatoló egy régió magas értékek a fázis az ellenkező értelemben. A röppálya ábrázoltuk 1. ábra mutatja eredetét a nyelv; folyékony részecskék, amelyek advected a közelben a belső henger az első θ katalógusa 1 lépés ezután advected szignifikánsan eltérő értéket r katalógusa a belső henger. Ennek eredményeként a folyadék részecske található egy teljesen más Streamline az első lépés, amikor a külső henger forogni kezd visszafelé. Mint az várható, a kisebb paraméterértékek ezt nyelv hiányzik (ábra a 2 (d)). Még magasabb értékek θ katalógusa, a másik viszont, (2. ábra (f)) a nyelv pakolások kétszer kerek egy rendkívül összetett módon. A 2. ábrán a (G) -2 (I) megmutatjuk, ábrázolva az evolúció egy sor kezdeti feltételeket, hogy a geometriai fázis összefügg a dinamikai struktúrák a áramlását. 2. ábra (g), a θ katalógusa = π katalógusa /2 radián, azt mutatja, hogy ha ez a nyelv hiányzik, a vonalszakasz alig fejlődik; az áramlás csaknem reverzibilis. A vonalszakaszok a 2. ábra (h) és a 2. (i), a θ katalógusa = 2 π katalógusa és 4 π katalógusa radián, a másik viszont azt mutatják, a nagy nyúlás okozta ezt a nyelvét a nagy geometriai fázis. Annak igazolására, ezt a hatást a geometriai fázis áramlási részletesebben, a 3. ábrán (b) azt a telek hossza a vonalszakasz után egy ciklus ellen a forgatás szögét. A jelentős aspektusa ez a parcella, hogy megjelenik fennsíkok elválasztott a gyors növekedés. Egy összehasonlítás ábra a 2 (d) -2 (F) azt mutatja, hogy ez a penetráció a nyelv a nagy értékek a geometriai fázis át ezt a szakaszt, hogy indukálja a nyújtás. A nyelv hatol előtt első alkalommal θ katalógusa = 2 π katalógusa, majd másodszor előtt θ katalógusa = 4 π katalógusa, így állítanak elő két ugrik; ezek között ugrik alakulását a vonalszakasz sokkal lassabb. Egy adott energia költség, amely bővíthető az összes jelöletlen elmozdulás a falak, geometriai keverés ezért hatékonyabb a nagy értéke θ katalógusa.
≈ 10 3 kg m 3 és a maximális áramlási sebesség V katalógusa megfigyelt tartományban 2,5-7,5 mm s -1 [21]. Ezekből az adatokból lehet becsülni a Reynolds-szám Re katalógusa = ρVL katalógusa / μ katalógusa feküdni a tartományban 0,2-0,5. Így azt mondhatjuk, hogy az emberi gyomorban folyadék tehetetlensége csak korlátozott jelentőséggel, és minden kisebb állat lesz jelentéktelen. Megjegyezzük, hogy a korábbi munka gyomor keverő többnyire tekintik esetében inerciális hozzájárulások [21, 23, 24], amelyek esetében a dinamikai korlátok itt tárgyalt nem kell alkalmazni. Katalógusa
/ ω katalógusa = 5 cm, és amplitúdója b katalógusa = 1/2 × 0,6 L katalógusa ≈ 2 cm. Ezek a hullámok kényszeríteni a gyomor keresztül nonreciprocal hurok a térben a formák, mint amelynek eredményeként geometriai keverés várható. Lehet durva becslést adni a várható mértékét, geometriai fázis kihasználva kapott eredmények egy másik geometriai fázis probléma: hogy az alacsony Reynolds-szám mikroorganizmusok úszás. Számos baktérium úszni deformálásával testüket ugyanúgy, mint a perisztaltikus hullámok a gyomor és a sebességet már jól becsülhető modellezési ilyen deformációk, mint sík hullámok [25]. Hasonló számításokat a gyomor teszi az áramlási sebesség által indukált perisztaltikus hullámok V katalógusa = πc katalógusa ( b katalógusa / λ katalógusa) 2 , ami jön ki körülbelül 1 mm-s -1, ahonnan egy elmozdulás körülbelül 6 cm per perisztaltikus ciklus várható, vagy, figyelembe véve, egy kör alakú gyomor sugarú L, a geometriai fázis nagyságrendű 2 radián.
, v katalógusa) a megfelelő peremfeltételek a perisztaltikus hullám a felső határ, u katalógusa = 0 és v katalógusa = ∂ z katalógusa w katalógusa /∂ t
z katalógusa = z katalógusa w katalógusa ( x katalógusa, t katalógusa), és a szimmetria peremfeltételek a z katalógusa = 0 . oldalfalak deformálódik függőlegesen, hogy megfeleljen a függőleges sebességét a perisztaltikus hullám x katalógusa = 0 és x katalógusa = 2 π katalógusa. Ábrán a 4 (a), fekete folytonos vonalak jelentik a áramvonalak az indukált folyadék mozgás belül az üreg miatt a perisztaltikus hullám. A kontúrgörbe megfelel az időben átlagolt sebesség több mint egy teljes perisztaltikus ciklust. Területek maximális átlagos sebesség közel vannak a szimmetria tengelye, mivel a fal mellett az átlagos sebesség nulla, és nem átlagos mozgás keletkezik. Katalógusa
»1 és légmozgások okozta járulékok uralják a keverési folyamatot. 4. ábra (c) képviseli a területi koncentráció a passzív skalár χ katalógusa után 20 perisztaltikus ciklus (vagyis egy skálázott idő T katalógusa = t katalógusa / T katalógusa * = 20, ahol a T katalógusa * jelenti a ciklus időszak) az Pe
= 15 × 10 3. Az áramlási által indukált perisztaltika halmozódik véges geometriai fázis után minden ciklusban, folyadék elemek vannak terhelve, és hajtva, és ennek következtében, vékony szálak vannak kialakítva, hogy megkönnyítik a keverési belül az üreget.
( x katalógusa, 0)]. Közötti euklideszi távolság a kezdeti és a végső helyzetben egy ciklus után becslést ad a geometriai fázis. Kontúrok ábrán a 4 (d) képviseli a geometriai fázisának a rendszert. Látható, hogy a maximális elmozdulások figyelhetők meg a központi régióban az üreg ahol szálak jönnek létre. Megjegyezzük, hogy a régiók ábrán a 4 (d) a kis elmozdulások megfelelnek az régiók maradnak nem kevert ábrán a 4 (c). Így és annak ellenére, hogy az egységes sugara az üreg a mi minimális geometriai modell, keverés nem térben egyenletes. Régiók a központi része az üreg alkot vékony szálak, hogy fokozzák a keverés, mivel a régiók közel a laterális és a felső falak maradnak szinte nem kevert 20 ciklus után. Még további inhomogenitása várhatóan több hűséges geometriák, változó átlagos fal átmérője [27], és bizonyos időzítési a nyitó és záró a pylorus a perisztaltikát [28] közötti kölcsönhatás a fundus /szív régióban a gyomor [29], az összes amelyek ismert funkció keverésére a gyomorban [30].
katalógusa forog szögsebességgel Ω katalógusa. Az excentricitás a belső henger adják ɛ katalógusa. A határ, ahol viszkózus erők elhanyagolhatók, a keletkező áramlás integrálásával kaptunk biharmonic egyenletet a patak funkció ∇ 4 ψ katalógusa = 0, a megfelelő peremfeltételek a falak a henger.
megfelel a megoldás a folyam funkció az áramlás által indukált belső henger. A szög által lefedett henger egy ciklus alatt függ szögsebesség szerint (2) ha a részindex i
jelöli a külső vagy belső henger és a T katalógusa * az időszak a ciklus . Mivel a szimulációk Ebben az írásban a szögsebessége hengerek állandó, Θ i
= T katalógusa * Ω i
. Ez az áramlás elismeri pontos megoldás [11], az adatfolyam funkciót, amikor a probléma meg van írva a bipoláris koordináták ( ξ katalógusa, η katalógusa). A Descartes-féle koordináta-rendszerben ( x katalógusa, z katalógusa) nyerhető szerint (3) ahol (4) A [11] a megoldás a belső és a külső áram funkciók adják (5 ), ahol H katalógusa = b katalógusa /( c katalógusa 2 + s katalógusa 2) 1/2, a s katalógusa = sin ξ katalógusa sin η katalógusa és c katalógusa = cosξ katalógusa cos η katalógusa - 1. Sőt, (6) (7) és (8) (9) withwhere ξ katalógusa katalógusa és ξ katalógusa ki
képviseli a felülete a belső és külső henger, illetve, és Δ,, Δ *, h katalógusa 1 h katalógusa 2, ..., H
8 által adott
, η katalógusa i
) találhatók ( ξ katalógusa f katalógusa, η katalógusa f katalógusa).
 A bőrön talált gyakori gomba gyulladásos bélbetegséget okozhat
A bőrön talált gyakori gomba gyulladásos bélbetegséget okozhat
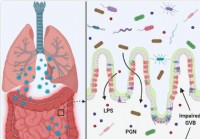 A szivárgó bél és a mikrobiális dysbiosis hozzájárulhat a citokin viharhoz súlyosan beteg COVID-19 esetekben
A szivárgó bél és a mikrobiális dysbiosis hozzájárulhat a citokin viharhoz súlyosan beteg COVID-19 esetekben
 A vörös hús növényi alapú húsra való cseréje csökkenti a szív- és érrendszeri kockázatot
A vörös hús növényi alapú húsra való cseréje csökkenti a szív- és érrendszeri kockázatot
 A kutatók új módszert találnak a betegségek elleni védekezésre az MS modellben
A kutatók új módszert találnak a betegségek elleni védekezésre az MS modellben
 A bélfokozó ételek világszerte véget vethetnek a gyermekkori alultápláltságnak
A bélfokozó ételek világszerte véget vethetnek a gyermekkori alultápláltságnak
 Cöliákia kezelése
Cöliákia kezelése
 Ez a Pepto valószínűleg nem segít a fekélyén
A peptikus fekély a nyelőcső nyálkahártyájában kialakuló seb vagy elváltozás, gyomor, vagy nyombél. Nemrég, azt feltételezték, hogy a fekélyeket az okozza, hogy valaki stresszes vagy egyszerűen túl so
Ez a Pepto valószínűleg nem segít a fekélyén
A peptikus fekély a nyelőcső nyálkahártyájában kialakuló seb vagy elváltozás, gyomor, vagy nyombél. Nemrég, azt feltételezték, hogy a fekélyeket az okozza, hogy valaki stresszes vagy egyszerűen túl so
 Emberek versus vírusok - El tudjuk kerülni a kihalást a közeljövőben?
Szakértő szerint az ember által okozott környezeti változások kórokozók megjelenéséhez vezethetnek, nemcsak kívülről, hanem a saját mikrobiomunkból is, amely utat nyithat az emberek nagyarányú megsemm
Emberek versus vírusok - El tudjuk kerülni a kihalást a közeljövőben?
Szakértő szerint az ember által okozott környezeti változások kórokozók megjelenéséhez vezethetnek, nemcsak kívülről, hanem a saját mikrobiomunkból is, amely utat nyithat az emberek nagyarányú megsemm
 A tüdő mikrobiomája megjósolja a COVID-19 betegség súlyosságát
Egy új előnyomtatási kutatási dokumentumot tettek közzé a medRxiv * A szerver változásokat talált a tüdő mikrobiomjában súlyos akut légúti szindróma koronavírus 2 (SARS-CoV-2) fertőzés hatására a CO
A tüdő mikrobiomája megjósolja a COVID-19 betegség súlyosságát
Egy új előnyomtatási kutatási dokumentumot tettek közzé a medRxiv * A szerver változásokat talált a tüdő mikrobiomjában súlyos akut légúti szindróma koronavírus 2 (SARS-CoV-2) fertőzés hatására a CO