En modell tidsserier av förekomsten av gastric dilatation-tarmvred i en population av hundar Bild Sammanfattning
Bakgrund
Gastric dilatation-tarmvred (GDV) är en livshotande tillstånd hos däggdjur, med ökad risk i stora ras hundkapplöpning. Studiet av dess etiologiska faktorer är svårt på grund av den mångfald av möjliga levnadsförhållandena. Sambandet mellan meteorologiska händelser och förekomsten av GDV har antagits men är fortfarande oklart. Denna studie presenterar den binära tidsserie strategi för undersökning av eventuella meteorologiska riskfaktorer för GDV. De data som samlas in i en population av högrisk arbetande hundar i Texas användes.
Resultat
Minimum och maximal daglig atmosfärstryck på dagen för GDV händelse och den maximala dagliga atmosfärstryck på dagen före GDV händelsen var positivt samband med sannolikheten för GDV. Alla odds /multiplikativa faktorer för en dag är GDV dag tolkades villkorligt på de senaste GDV händelser. Det var minimal skillnad mellan de binära och Poisson generella linjära modeller.
Slutsats
Tidsserier modellering som en ny metod för att utvärdera sambandet mellan meteorologiska variabler och GDV i en stor population av hundar. Lämplig tillämpning av denna metod har förbättrats genom en gemensam miljö för hundarna och tillgången på meteorologiska data. Den potentiella interaktionen mellan väderomslag och patient riskfaktorer för GDV förtjänar ytterligare utredning.
Bakgrund
Gastric dilatation-tarmvred (GDV) är ett tillstånd där magen vidgar och roterar på sig själv, vilket leder gradvis till hypotension, chock, och död. Stora hundar ofta påverkas, även om det kan påverka många djurarter inklusive människor [1]. Sälja The fysiska mekanismer som är involverade i detta tillstånd och dess behandling är väl förstått, men orsakerna är inte [2]. Orsaker till GDV kan betraktas predisponerande (ökar sannolikheten för sjukdom) eller utfällning (utlöser uppkomsten av sjukdomen). Flera predisponerande riskfaktorer hos hundar har föreslagits, inklusive temperament på hunden (retbarhet), stor eller jätte ras, ökad bröst djup till bredd och snabb livsmedelskonsumtion [2-4]. Men många frågor relaterade till själva uppkomsten av denna livshotande sjukdom förblir oförklarade av dessa riskfaktorer.
Studie av utfällning orsaker till GDV är en viktig och inte mycket väl utforskade området. I många fall av GDV, är magen utspänd med gas; bland möjliga källor för denna gas, Aerofagi, jäsning-förruttnelse, kemisk gas genes och gas diffusion har föreslagits. Detta, i kombination med observerade säsongsvariation i GDV fall gav upphov till misstankar om möjliga samband mellan GDV och väderförhållanden strax innan dess förekomst [5, 6]. Metoder som tillämpas av Herbold et al [5], det vill säga huvudkomponenter analys, för att välja eventuellt viktiga climatologic faktorer kan ha fördunklat effekterna av en enda väderrelaterade variabel. Andra studier har använt logistisk regression för att undersöka sannolikheten för en dag att vara en GDV dag, givet vissa atmosfärstryck eller temperaturbetingelser [6, 7]. Sådana metoder är baserade på en premiss som GDV händelser är oberoende av varandra och det finns ingen stark korrelation mellan händelser under en tidsperiod, som skulle uppstå om sjukdomen var smittsam. Men som i själva verket de flesta meteorologiska variablerna tros påverka GDV förekomst är autokorrelerade över tiden och bör ses som tidsserier. Om några av dem inte har tagits med i en tänkbar modell, men de påverkar GDV förekomst, kan GDV incidenter noterats under tiden korreleras.
Således tittar på GDV uppgifter om förekomsten som tidsserier kan vara lämpligt i praktiken. Även traditionella tidsserier modellering har haft begränsad tillämpbarhet i studiet av ovanliga sjukdomar, har det nyligen använts för att demonstrera en säsongskomponent till en annan gastrointestinal sjukdom, nämligen kolik hos hästar [8]. Eftersom förekomst uppgifter GDV är tydligt heltal värderas (värdet av svaret är antalet GDV fall per dag), de mer traditionella tidsseriemetoder, såsom de som används i den klassiska Autoregressive Integrated Moving Average (ARIMA) ram [9] kan inte användas. En av de tidigare referenserna [8] antyder att "... En möjlighet ligger i användningen av en Poisson-fördelning för att modellera data count inom en ram i stort sett analogt med det i generaliserad linjär modellering ..."; detta förslag uppgår effektivt till att använda den metod som grundar sig på allmän linjär modell (GLM) ramverk som används i detta manuskript.
Syftet med denna studie var att använda en tidsserie strategi för att undersöka sambandet mellan meteorologiska variabler och GDV förekomst hos hundar. För att minska variabiliteten av predisponerande riskfaktorer och störande variabler såsom kost och boendemiljö [2], var dataset stora hundar inhysta på militära arbetet Hund (MWD) Training Center vid Lackland Air Force Base (LAFB) används. I denna gemensamma miljö, är hundar som fick en standarddiet, inrymt i utomhus körningar, och är under observation 24 timmar om dygnet. Denna datamängd har använts tidigare i en logistisk regressions metod för att undersöka meteorologiska variabler och GDV [7], och en jämförelse av de metodologiska angreppssätt kan därför också göras.
Resultat
Flera modeller som hade några av de lägsta värdena av AIC (Akaike Information Criterion) visas i Tabell 1. för varje av dem är den systematiska delen ges tillsammans med den typ av modell (binära GLM eller Poisson GLM) och värderingar av AIC. Endast modeller som hade log-sannolikhetsförhållande p-värden för alla kovariater under 0,10 hade inkluderats. Eftersom hunden räkningen varierar från dag till dag, är mängden exponering närvarande variabel. Detta kan göra strikt Poisson /binär antagande om uppgifterna orealistiska. I Poisson fallet innebär detta att variansen inte kan vara exakt lika med medelvärdet. I det binära fallet kan variansen inte är exakt lika med variansen för bernoullifördelning för en given uppsättning av kovariateffekter värden. Således verkar det rimligt att leta efter möjliga spridning i data. En enkel kvasi-sannolikhet tillvägagångssätt användes för att leta efter tecken på överspridning [10]. Den beräknade koefficienten är alltid nära till ett och därför verkar det inte vara någon allvarlig tecken på överspridning i denna setting.Table 1 Den slutliga modeller
Modell
Systematisk del
Typ av modellen
AIC
spridning faktor
en
β
0 + β
1Y
t
-2 + β
2pmin
t
Binary GLM
411,02
1,02 2
β
0 + β
1Y
t
-2 + β
2pmin
t
Poisson GLM
407,92
0,98
3
β
0 + β
1Y
t
-2 + β
2pmax
t
-1
Binary GLM
406,47 1
4
β
0 + β
1Y
t
-2 + β
2pmax
t
-1
Poisson GLM
403,42
0,95
5
β
0 + β
1Y
t
-2 + β
2pmax
t
Binary GLM
410,46
1,02
6
β
0 + β
1Y
t
-2 + β
2pmax
t
Poisson GLM
407,40 0,97
Undersökning av restautokorrelations tomter indikerade att arbets residualerna autokorrelations tomter var nästan identiska, och alla av dem inte visar någon väsentlig kvarvarande autokorrelation. Baserat på detta, dessa tre modeller verkar ge en tillräcklig passning för GDV förekomsten data Y
t
. Sälja The koefficienterna i dessa modeller tolkades som antingen log odds (OR) i binär GLM modeller eller multiplikativa faktorer (MF) i Poisson GLM modeller. Tabell 2 innehåller värdena för oddskvoten och multiplikativa faktorer för eftersläpande respons Y
t
-2 och externa kovariat för alla modeller från tabell 1. Den innehåller också log-sannolikhets p-värden för alla oddskvoterna. I namnen på kolumnerna i tabell 2, eller stå för oddskvot och MF för den multiplikativa faktorn; "andra kovariat ELLER" är antingen minsta dagliga atmosfärstryck på GDV dag pmin
t
, den maximala dagliga atmosfärstryck på GDV dag pmax
t
eller den maximala daglig atmosfärstryck på dagen före GDV dag pmax
t
-1. LL står för log-sannolikhet. Eftersom sannolikheten för GDV händelse på en viss dag är liten och värdena hos hunden räkningen är i hundratals, kan modellen vara lämpligt som antingen binära GLM eller Poisson GLM. Båda metoderna används för jämförelseändamål. Det var mycket liten skillnad mellan den binära GLM och Poisson GLM i fallet för alla uppsättningar av covariates considered.Table 2 Modell Selection
Modell
OR Y
t
-2
LL p-värde
Andra kovariat ELLER /MF
LL p-value
1
3.1606
0.0595
1.0455
0.0891
2
3.0862
0.0640
1.0464
0.0833
3
2.9492
0.0741
1.0663
0.0064
4
2.8711
0.0807
1.0664
0.0062
5
3.0198
0.0693
1.0456
0.0633
6
2.9498
0.0741
1.0460
0.0606
Among Den sista gruppen av modeller som visas fanns ingen som anses externa covariates vid eftersläpning mer än en dag. Sådana modeller ansågs under modellurvalsfasen, dock. I samtliga dessa fall släpar log-sannolikhetsförhållandet p-värde på den externa kovariat av mer än en dag var betydligt högre än 0,10, medan koefficienten för två dagars fördröjning av svaret Y
t
-2 hade log-sannolikhetsförhållandet p-värde konstant under 0,10. Således är valet av kovariater inte partisk till förmån för de eftersläpningar av respons Y
t-delar på bekostnad av externa kovariat släpar.
Baserat på dessa modeller, verkar det som de faktorer som påverka graden av GDV mest märkbart är således det minsta dagliga atmosfärstryck på dagen för GDV händelse, den maximala dagliga atmosfärstryck på dagen för GDV händelse och den maximala dagliga atmosfärstryck på dagen före GDV händelsen. Oddskvoterna /multiplikativa faktorer i yttre kovariat i alla modeller är något större än en som indikerar positivt samband mellan dessa faktorer och sannolikheten för GDV händelse på en viss dag. Till exempel har den minsta dagliga atmosfärstryck på dagen för GDV händelse en oddskvot 1,0455 för den binära GLM modell. Detta tyder på att för varje ökning av minimi dagliga atmosfärstryck med en enhet, oddsen för GDV fall inträffar den dagen ökar med faktorn 1,0455. För respektive Poisson modellen, är den multiplikativa faktorn 1,0464 vilket innebär att för varje ökning av minimi dagliga atmosfärstryck genom en enhet sannolikheten för dagen är en GDV dag blir multipliceras med faktorn 1,0464. Observera att alla resultat för den externa kovariat bör tolkas villkorligt på vad som hände två dagar före observationen dag. Således är det mer exakt att säga att oddsen för GDV händelse på en viss dag ökar med faktorn 1,0617 för varje enhet ökning av minimi dagliga atmosfärstryck med tanke på att vi vet om det fanns eller inte var ett fall av GDV två dagar tidigare
. Ovanstående uttalande kan inte göras utan att veta vad som hände två dagar före dagen för observation. Detta är den viktiga skillnaden mellan vår strategi och att den vanliga GLM modellering, om binär GLM (logistisk regression) eller en Poisson modell Diskussion och slutsats
Först.
Varje modell valda tillhandahålls viktig information om möjliga etiologisk faktor GDV och därmed spelar en viktig roll. Det är inte nödvändigt att göra ett val mellan dem om det enda syftet är att undersöka möjliga förklarande kovarians för GDV händelse. Men blir det nödvändigt om prognostisering av framtida GDV incidenter är huvudfokus. Vi undersöker inte denna fråga i den aktuella papper.
Andra variabler som identifierats som faktorer väsentligt påverkar graden av GDV händelse var det minsta dagliga trycket på dagen för GDV, den maximala dagliga trycket på dagen för GDV och maximala dagliga trycket på dagen före GDV händelse. Minsta dagliga tryck på dagen för GDV också identifierats som viktiga och statistiskt signifikanta faktorer i [7]. Det är känt att det finns samband mellan förändringar i lufttrycket och förlossning hos människor och SIDS (plötslig spädbarnsdöd) [11, 12]. Mindre är känt om sambandet mellan atmosfärstrycket och hund sjukdomar. Den aktuella studien visar att atmosfärstrycket och förändringar i det kan vara de viktigaste faktorerna som förklarar uppkomsten av GDV hos hundar.
Värdet på en 2-dagars fördröjning svar i modellering för GDV var något oväntat. Detta 2-dagarsperiod inte nödvändigtvis korrelerar med en 48-timmarsperiod mellan händelser, dock. Den exakta uppkomsten av kaskad av händelser som leder till GDV är svårt att avgöra, och patofysiologiska händelser som leder till kliniska tecken kan förekomma i olika takt i olika hundar. Gastric buk har noterats att ske snabbt i vissa hundar, och långsammare i andra. Den roll som kovariater som kan kopplas till förseningar i klinisk manifestation, liksom möjliga förhållande (n) bland meteorologiska fenomen under en sådan tidsfönster, återstår att belysas.
Tillvägagångssätt med hjälp av logistisk modell för binär tid serien verkar vara tillräcklig i de fall där det finns högst några dagliga observationer med mer än en GDV fall. Emellertid kan detta inte vara fallet om en större grupp av hundar observeras och, som en konsekvens, antalet dagar med mer än ett fall av GDV blir betydande. Om detta händer, kan Poisson GLM tillvägagångssätt måste användas exklusivt. Review, en relaterad papper [8] använder den latenta variabel modellering baserad på den hierarkiska Bayes metod för att införliva beroendet mellan observationerna. Detta tillvägagångssätt är något mindre flexibla än den metod som förespråkas i detta dokument. Anledningen är att den hierarkiska Bayesian metod kräver vissa tidigare antaganden, såsom normalitet (eller annan särskild fördelning) av uppgifterna, som inte alltid är lätt att motivera i praktiken. Dessutom verkar valet av ordern en autoregressiv process för den latenta variabeln att vara subjektiv och grundar sig inte på någon särskild modell val algoritm Denna forskning ger en inblick i den möjliga val som grundar sig på kriterier som AIC. Slutligen är det viktigt att notera här att den tidsserie tillvägagångssätt är mycket naturligt när det finns serier av observationer inspelade över tiden. Om det händer, är sådana observationer nästan alltid korrelerade; ignorera denna korrelation kan leda till förvrängda slutsats om parametrar av intresse. I synnerhet, ofta resulterar det i överdrivna nivåer av betydelse för förklarande variabler. Därför tidsserien baserade metoden är förmodligen den lämpliga forskningsverktyg i många kliniska studier där observationerna har registrerats under en tidsperiod.
Metoder
Data
GDV förekomst datapost består av alla registrerade fall av GDV bland de militära arbetande hundar (MWD) vid Lackland Air Force Base (LAFB) från januari 1993 till december 1998. i varje fall rasen drabbade hund, dess kön, födelsedatum, ålder vid uppkomsten av sjukdomen och vikten registrerades. Alla hundar var av en av tre raser: Tysk herde, belgisk Malinois, eller holländska Shepherd. Den första konstaterade fallet av GDV inträffade jan 6, 1993 och den sista den 25 december 1998. Det totala antalet registrerade fall (dvs. de dagar som GDV fall registrerades) är 60 av 60, bara två dagar inblandade mer än ett fall av GDV; på dem båda, det fanns 2 drabbade hundar. Alla kenneled hundar kontrollerades av personal var 3 timmar per organisatoriska standardförfaranden. Fall var hundar som visade svullen buk, tympani i magen, och radiografiska tecken på gastric dilatation som bestäms av en veterinär. Kirurgiskt ingrepp inleddes i alla fall, antingen på grund av livshotande tillstånd eller för icke-akuta profylaktisk gastropexy förfarande.
Antalet hundar under observation på LAFB var inte konstant utan förändras från månad till månad. Den månatliga hund räkningen uppgifter fanns oktober 1993 genom Dec 1997 endast, börjar med 357 hundar i oktober 1993 och slutar med 281 hund i december 1997. På grund av avsaknad av folkräkningsuppgifter för 1998, GDV uppgifter om förekomsten för det året användes inte.
En stor databas av väderdata samlades från National Climatic Data Center vid Kelly Air Force Base, som ligger i direkt anslutning till LAFB. Den innehöll timvärden på vindriktning, hastighet och vindby; hourly temperatur i Fahrenheit grader, både justeras och ojusterade för fuktighet och, slutligen, atmosfärstryck i inches of mercury, båda anpassas till havsnivån, och ojusterade en (i millibar).
Modellering tillvägagångssätt Review, en rad möjliga modeller för GDV förekomst i hundpopulationen ansågs. I samtliga av dem, var förekomsten av GDV på en viss dag kodas med hjälp av en för en GDV dag eller 0 för en icke-GDV dag och används som ett svar variabel. Andra kvantiteter, såsom, till exempel, atmosfärstryck och lufttemperatur, användes som prediktorvariabler. Den binära svarsdata lämpar sig för ett antal möjliga metoder, bland annat binär GLM med logistiklänkfunktionen (logistisk regression) och en Poisson GLM med en logg länk funktion (Poisson regression) Review Både respons och kovariater registrerades över tiden. detta gör det rimligt att visa både svaret och kovariater som tidsserier. I stället för den vanliga generaliserad linjär modell som förutsätter uppgifterna är IID, vi utnyttjade modifierad form av det där både svar och covariates är autokorrelerade över tiden.
Dessutom är en tidsserie metod användbar i den här inställningen, eftersom det är ganska troligt att ett antal väderrelaterade (och eventuellt andra) covariates redovisas inte, ett stort antal möjliga etiologiska faktorer gör det ganska svårt att inkludera alla dem i en modell. Förutom lufttemperatur och atmosfärstryck som ansågs tidigare, luftfuktighet (antingen absolut eller relativ) kan vara en av de möjliga etiologiska faktorer. Luftfuktighet registreras över tid och oftast uppvisar märkbar autokorrelation. Typiskt är det tänkt som en tidsserie; om responsvariabeln är verkligen beroende av fuktighet, orsakar dess utelämnande responsvariabeln uppvisa tidsautokorrelation. Denna tankegång tyder på att en tidsseriemodellen inom ramen GLM kan bli bättre på att beskriva GDV förekomst än den vanliga logistik GLM modell anses i [7]. Andra covariates som ofta nämns som de sannolika möjliga etiologiska faktorer för GDV, såsom atmosfärstryck, lufttemperatur och andra, är också slumpmässiga tidsberoende kovariater (tidsserier) själva. Således, utelämnandet av någon av dem
är sannolikt att framkalla ytterligare autokorrelation i svaret.
Ut av flera möjliga modelleringsmetoder, denna forskning använde en som bygger på att sätta heltal värderas tidsserier i den generaliserade linjära modell ram [13]. Till skillnad från den tidigare Markov kedjan strategi, inte medföra att antalet parametrar som skall beräknas växa exponentiellt med provstorleken; Det är också tillräckligt bred för att omfatta de flesta av de praktiskt viktiga modeller. Observera att varken egendom Markov eller stationärt måste antas vid användning av denna metod. Detta är viktigt eftersom båda av dessa egenskaper kan vara svåra att kontrollera i praktiken. De resulterande modeller kan beräknas med samma metod (iterativ viktas minsta kvadrat, IWLS för kort) som vanliga generaliserade linjära modeller; den enda skillnaden är att resultaten måste tolkas villkorligt på det förflutna.
GDV förekomst på dag t
betecknades som Y
t
. Således, Y
t
var binärt. De kovariater kan omfatta tidigare och nuvarande värden för förklaringsvariabler samt tidigare värden på Y
t
. Vektorn av alla kovariater betecknades som där p
är antalet kovariater, k
antalet förklarande variabler släpar och q
antalet tidigare släpar av Y
t
betraktas; för varje 1 ≤ i
≤ p Mössor och en ≤ j
≤ k
, representerade värdet av i
th kovariat vid tiden t
- j
. Sannolikheten för en GDV fall på en viss dag definierades som p
t
som också är en funktion av den kovariat vektorn z
t
. Det finns åtminstone två möjliga sätt att modellera sannolikheten för GDV på en viss dag. Det första valet är att använda den binära GLM med logit länkfunktionen - på ett effektivt sätt, en logistisk regressionsmodell. Den slumpmässiga komponenten i modellen är sedan en vektor av binära värden för Y
t
som autokorrelerade över tiden. Den systematiska komponenten i den resulterande logistikmodell blir (1) där α
är intercept, β
är vektorn av koefficienter och p
t
är sannolikheten för GDV händelsen på en viss dag t
som beror på uppsättningen kovariater z t
. För varje GDV dag, är sannolikheten för händelsen definieras som antalet fall som observerats på den dagen dividerat med den totala befolkningen i hundar som spelats in på samma dag. Eftersom alla GDV sannolikheter var små i studien, är det också möjligt att modellera sannolikheten för GDV händelse på en viss dag t
använda Poisson regression. Detta innebär att den slumpmässiga komponenten i modellen är en vektor Y
t
som betraktas nu som Poisson räknas. Den systematiska komponenten i modellen avser det genomsnittliga antalet fall på dag t μ
t
till variablerna med log länk som (2) där, ännu en gång, är α
intercept, β
är vektorn av koefficienter och μ
t
beror på uppsättningen kovariater z t
som tidigare.
som ett första steg i proceduren för val av modell , de dagliga egenskaper, såsom max, min och medelvärdet, av det atmosfäriska trycket och lufttemperatur ansågs vara möjliga variablerna. Temperaturen justerades inte för fukt. De eftersläpande värdena för atmosfärstryck och /eller temperatur kan ses som möjliga GDV etiologiska faktorer och på så sätt ytterligare förklarande variabler samt. Sannolikheten-ratio test användes för att kontrollera statistisk signifikans av modell variablerna. Förklaringsvariabler som skulle användas som en del av z t
valdes. Låt oss beteckna den minsta dagliga atmosfärstryck på en viss dag pmin
t
, maximal daglig atmosfärstryck pmax
t
, maximal daglig atmosfärens temperatur tmax
t
och lägsta dagliga lufttemperaturen tmin
t
. Tidigare värden (en dag innan) av ovanstående var pmin
t
-1, pmax
t
-1, tmax
t
-1 och tmint
t
-1. Den maximala timme höjning /sänkning av atmosfärstrycket på dagen för GDV händelsen betecknas rp
t Mössor och dp
t
, respektive medan den maximala timme höjning /drop i temperaturen på dagen för GDV händelsen betecknas rt
t Köpa och dt
t
. Hundarnas ras ansågs inte eftersom hundpopulationen var ganska homogen bestående av tre stora raser som rutinmässigt används som MWD. Alla icke-händelse dagar ansågs i denna analys också.
Modellerna konstruerades med användning av processen för stegvis framåt val. De kovariater tillsattes successivt och log-sannolikhetsförhållandet för varje ny kovariat beräknas. För att undvika förtida stopp, även om kovariat inte lägga mycket till beskrivande förmåga modell, mätt som dess log-sannolikhet förhållande statistik fortsatte processen tills alla kovariater beskrivits tidigare hade prövats. Antalet laggar Y
t
ingår i berörda modeller i denna forskning begränsades till 3 för att garantera parsimoniousness av modellerna. De rester av varje modell kan senare analyseras för autokorrelationsmönster och ytterligare eftersläpningar, om nödvändigt. Koefficienterna Y
t
-1 och Y
t
-3 hade mycket stor log-sannolikhet förhållandet p-värden oavsett vilken externa variablerna ingick i modellen; närmare bestämt deras log-sannolikhetsförhållande p-värden än 0,1 allt och därmed uteslöts från de slutliga modellerna. sälja The modeller som valts ut som slut visas i tabellen (1). Utom den minsta atmosfärstryck på GDV dag och den maximala atmosfärstryck på dagen för GDV händelsen och dagen före GDV händelsen, alla andra externa covariates visar log-sannolikhetsförhållande p-värden över det valda tröskelnivån 0,10 är inte ingår.
 Vad är problemet med hepatit C?
Vad är problemet med hepatit C?
 Hushållens desinfektionsmedel kan bidra till fetma hos barn
Hushållens desinfektionsmedel kan bidra till fetma hos barn
 Genetisk risk för autoimmunitet kan vara kopplad till skillnader i tarmmikrobiom
Genetisk risk för autoimmunitet kan vara kopplad till skillnader i tarmmikrobiom
 Tillväxtproblem hos prematura barn i samband med förändrade tarmbakterier
Tillväxtproblem hos prematura barn i samband med förändrade tarmbakterier
 Ulcerös kolit och en saknad mikrob i tarmen
Ulcerös kolit och en saknad mikrob i tarmen
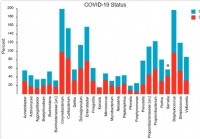 Sammansättning och struktur för nasofaryngeal mikrobiom relaterar till allvarlighetsgraden av COVID-19
Sammansättning och struktur för nasofaryngeal mikrobiom relaterar till allvarlighetsgraden av COVID-19
 Spermamikrobiom avslöjades med RNA -sekvensering
En ny studie rapporterar den första detaljerade beskrivningen av det mänskliga spermiemikrobiomet, med nyare RNA -sekvenseringstekniker som kan skilja mellan spermier -RNA och bakteriell kontaminering
Spermamikrobiom avslöjades med RNA -sekvensering
En ny studie rapporterar den första detaljerade beskrivningen av det mänskliga spermiemikrobiomet, med nyare RNA -sekvenseringstekniker som kan skilja mellan spermier -RNA och bakteriell kontaminering
 Förstå halsbränna
Halsbränna, den brännande känslan som uppstår antingen i bröstet eller halsen, är vanligtvis ett tillfälligt problem - kanske åt du kryddig mat - men för vissa människor, det kan vara kroniskt. Halsbr
Förstå halsbränna
Halsbränna, den brännande känslan som uppstår antingen i bröstet eller halsen, är vanligtvis ett tillfälligt problem - kanske åt du kryddig mat - men för vissa människor, det kan vara kroniskt. Halsbr
 Är C-sektionen bra för barns hälsa?
En ny studie publicerad av VATT Institute for Economic Research tyder på att en oplanerad CS utfördes för en indikation som kanske kunde ha undvikits, har bara en orsak-effekt-relation med astma från
Är C-sektionen bra för barns hälsa?
En ny studie publicerad av VATT Institute for Economic Research tyder på att en oplanerad CS utfördes för en indikation som kanske kunde ha undvikits, har bara en orsak-effekt-relation med astma från