Serija modela čas nastanka želodčne raztezanja-volvulus v populaciji psov
Abstract
Ozadje
želodca dilatacija-volvulus (GDV) je smrtno nevarno stanje sesalcev, s povečanim tveganjem za velike pasme psi. Študija njegovih vzročne dejavnike je težko zaradi različnih možnih življenjskih pogojev. Povezava med meteoroloških dogodkov in pojava GDV za katerega se domneva, vendar je še vedno nejasno. Ta študija predstavlja binarno čas serije pristop k preiskavi možnih vremenskih dejavnikov tveganja za GDV. Podatki, zbrani v populaciji z visokim tveganjem delovni psi v Teksasu je bila uporabljena.
Rezultati
minimalni in maksimalni dnevni atmosferski pritisk na dan GDV dogodka in največji dnevni atmosferskega tlaka na dan pred dogodkom GDV so pozitivno povezana z verjetnostjo GDV. Vse odds /multiplikativnih faktorjev dan čemer GDV dan razlagal pogojno na zadnjih GDV dogodkih. Prišlo je minimalna razlika med dvo- in Poissonovo splošnih linearnih modelov.
Zaključek
modeliranje časovnih serij pod novo metodo za ocenjevanje povezavo med meteorološkimi spremenljivkami in GDV v veliki populaciji psov. Primerno Uporaba te metode je okrepljeno s skupno okolje za pse in razpoložljivost meteoroloških podatkov. Potencial interakcije med vremenske spremembe in dejavniki tveganja, pacient za GDV zasluži nadaljnjo preiskavo.
Ozadje
želodca dilatacija-volvulus (GDV) je stanje, v katerem je želodec širi in se vrti na sebi, ki postopoma vodijo k hipotenzija, šok, in smrt. Velike pasme psov so pogosto prizadeti, čeprav lahko to vpliva na številne živalske vrste, vključno z ljudmi [1].
Fizikalne mehanizme, ki sodelujejo v tem stanju in njenem zdravljenju dobro razume, vendar pa so vzroki niso [2]. Vzroki za GDV se lahko šteje predispozicije (povečuje verjetnost bolezni) ali obarjanje (sproži pojav bolezni). Predlaganih je bilo več dejavnikov predispozicije tveganja pri psih, vključno temperament psa (razdražljivost), velike ali velikan pasme, povečana prsne globino in širino razmerje, in hitro porabo hrane [2-4]. Vendar pa je veliko vprašanj, povezanih z dejanskim nastopom te življenjsko nevarne bolezni, ostaja nepojasnjena teh dejavnikov tveganja.
Študijo obarjanje vzroke je GDV pomembna in ne zelo dobro raziskano področje. V mnogih primerih GDV, želodec je napihnjen s plinom; Med možnimi viri tega plina, aerofagija, fermentacija, gnitje, kemična plin geneza in difuzija plina je bilo predlagano. To, skupaj s opazovanem sezonskih nihanj v primerih GDV, je prišlo do sumov o morebitni povezanosti med GDV in vremenskih razmer tik pred pojavom [5, 6]. Metode, ki jih Herbold et al v [5], glavne komponente tj analize, ki se uporabljajo, da izberete možnosti pomembni klimatoloških dejavniki so lahko zameglil vpliv ene spremenljivke z vremenom. Druge študije so uporabili logistično regresijo, da razišče verjetnost dan pomeni GDV dan, ki ga nekateri atmosferski tlak ali temperatura pogojev [6, 7]. Takšni pristopi temeljijo na predpostavki, da so GDV dogodki med seboj neodvisni in ne obstaja močna povezava med dogodki v daljšem časovnem obdobju, kot bi se zgodilo, če bi bila bolezen nalezljiva. Vendar pa, kot je pravzaprav večina meteorološki spremenljivki mislili, da vplivajo GDV pojav, so autocorrelated več časa in jih je treba misliti kot časovne vrste. Če nekateri od njih niso bile vključene v potencialnega modela, vendar pa vplivajo na pojav GDV lahko GDV pojavnost posnete s časom korelaciji.
Tako si podatke GDV dogodkih kot so časovne vrste se priporoča v praksi. Čeprav je tradicionalna časovne serije modeliranje imel omejeno uporabnost v študiji občasni bolezni, je bilo v zadnjem času uporablja za dokazovanje sezonsko komponento na drugo boleznijo prebavil, in sicer, kolike pri konjih [8]. Ker se podatki pojav GDV jasno celo vrednotijo (vrednost odziva je število GDV primerov na dan), bolj tradicionalne metode časovne serije, kot se uporabljajo v klasičnem Autoregresivni integrirane Moving Average (ARIMA) okvir [9] se ne sme uporabljati. Eden od prejšnjih referenc [8] kaže, da je "... Ena možnost je v uporabi Poissonove porazdelitve na podatkovnem modelu štetje v okviru splošno analogen tistemu iz generalizirane linearnega modeliranja ..."; ta predlog dejansko pomeni, da s pristopom, ki temelji na generalizirane linearnega modela okvira (GLM), ki je v uporabi v tem rokopisu.
Cilj te raziskave je bil uporabiti pristop časovno serije raziskati povezavo med meteorološkimi spremenljivkami in GDV pojava pri psih. Za zmanjšanje variabilnosti predispozicije dejavnike tveganja in kompleksno spremenljivk, kot so prehrana in stanovanjsko okolje [2], je bila uporabljena nabor podatkov o velikih pasem psov, ki so nastanjene v delovni pes vojaškega (MWD) Training Center na Lackland Air Force Base (LAFB). V tem skupnem okolju, so psi hranijo standardno dieto, nameščene na prostem teče, in so pod nadzorom 24 ur na dan. Ta nabor podatkov je bila uporabljena, preden v logistično regresijsko pristopa k preiskovanju meteoroloških spremenljivk in GDV [7], in se zato lahko tudi primerjava metodoloških pristopov.
Rezultati
več modelov, ki so imele nekatere od najnižjih vrednosti o so AIC (Akaike Informacije Merilo), je prikazano v tabeli 1. za vsako od njih, se sistematično del, skupaj z vrsto modela (binarni GLM ali Poissonove GLM) in vrednot DIP. so bili vključeni le modeli, ki so imeli za prijavo katerih verjetnost razmerje p-vrednosti vseh spremenljivk pod 0,10. Ker je pes popis se spreminja iz dneva v dan, se količina izpostavljenosti je spremenljiva. To lahko strogo Poisson /binarno domnevo o podatkih nerealno. V primeru Poissonove, to pomeni, da se varianca ne morejo biti povsem enak povprečnemu. V binarnem primeru varianca ne morejo biti povsem enaka variance Bernoulli porazdelitve za določen niz sospremenljivko vrednosti. Zato se zdi smiselno, da preverite morebitne overdispersion v podatkih. Enostavni pristop kvazi-verjetnost je bila uporabljena za iskanje dokazov o overdispersion [10]. Ocenjeni koeficient je vedno blizu 1 in s tem se ne zdi, da bi vsak resen dokaz overdispersion v tem setting.Table 1 Končni Modeli
Model
sistematičnega dela
Tip modela
AIC
Overdispersion dejavnik
1
β
0 + β
1 leto
t
-2 + β
2pmin
t
Binary GLM
411,02
1.02
2
β
0 + β
1Y
t
-2 + β
2pmin
t
Poisson GLM
407,92
0,98
3
β
0 + β
1Y
t
-2 + β
2pmax
t
-1
Binary GLM
406,47
1
4
β
0 + β
1Y
t
-2 + β
2pmax
t
-1
Poisson GLM
403,42
0,95
5
β
0 + β
1Y
t
-2 + β
2pmax
t
Binary GLM
410.46
1.02
6
β
0 + β
1Y
t
-2 + β
2pmax
t
Poisson GLM
407,40
0,97
Pregled preostalih avtokorelacije parcel je pokazala, da so delovne ostanki avtokorelacija parcele skoraj enaki, in vse od njih ni pokazal nobene bistvene preostali avtokorelacija. Na podlagi tega se zdi, da so ti trije modeli, da zagotavljajo ustrezno prileganje za GDV podatki pojav Y
t
.
Koeficiente v teh modelih so bile razlagati tako, da bodisi log kvotami (OR) v binarnem GLM modelov ali multiplikativni dejavniki (MF) v Poisson GLM modelov. Tabela 2 vsebuje vrednosti razmerij obetov in multiplikativne dejavnike za zaostajala odziva Y
t
-2 in zunanji hkratna za vse modele iz tabele 1. Vsebuje tudi Log-katerih verjetnost p-vrednosti za vse razmerij obetov. V imeni stolpcev tabele 2, ali stoji za razmerje obetov in MF za multiplikativni faktor; »drugega hkratna ALI" je bodisi minimalna dnevna atmosferski pritisk na GDV dan pmin
t
, največji dnevni atmosferski tlak na GDV dan pmax
t
ali maksimalno dnevno atmosferski pritisk na dan pred GDV dan pmax
t
-1. LL stoji za log-verjetnost. Ker je verjetnost, da GDV dogodka na kateri koli dan majhna in vrednosti popisa psa v stotine, lahko model je primeren bodisi kot binarni GLM ali Poissonove GLM. Oba pristopa sta zaposleni za primerjavo. Tam je bilo zelo malo razlike med binarno GLM in Poissonove GLM v primeru za vse sklope spremenljivk considered.Table 2 Model Izbor
Model
ALI Y
t
-2
LL p-vrednost
Drugo kovariablo ALI /MF
LL p-value
1
3.1606
0.0595
1.0455
0.0891
2
3.0862
0.0640
1.0464
0.0833
3
2.9492
0.0741
1.0663
0.0064
4
2.8711
0.0807
1.0664
0.0062
5
3.0198
0.0693
1.0456
0.0633
6
2.9498
0.0741
1.0460
0.0606
Among zadnja skupina modelov je prikazanih bilo nobenega, ki obravnavajo zunanje Kovariable na zamika več kot 1 dan. Takšni modeli so bili v fazi izbora modela šteje, pa je. V vseh teh primerih je razmerje log-verjetnost p-vrednost zunanjega kovariablo zaostaja za več kot 1 dan je bil precej nad 0,10, medtem ko je koeficient 2-dnevnim zamikom od odziva Y
t
-2 imel razmerje log-verjetnost p-vrednost ves čas pod 0,10. Tako je izbira spremenljivk ne pristranski v korist zamikov odzivni Y
t
na račun zunanjega sospremenljivko zaostaja.
Na podlagi teh modelov, se zdi, da dejavniki, ki vplivajo na stopnjo GDV najbolj opazno sta tako minimalna dnevna atmosferski tlak na dan GDV dogodka, največjega dnevnega atmosferskega tlaka na dan GDV dogodka in največji dnevni atmosferskega tlaka na dan pred dogodkom GDV. Razmerja obetov /multiplikativni dejavniki zunanjega kovariablo v vseh modelih so nekoliko večji od 1, kar kaže na pozitivno povezavo med temi dejavniki in verjetnosti dogodka GDV na določen dan. Na primer, minimalna dnevna atmosferski tlak na dan GDV primeru ima razmerje verjetnost 1.0455 za binarnega modela GLM. To pomeni, da se za vsako povečanje minimalnega dnevnega atmosferskem tlaku za 1 enoto, je verjetnost primeru GDV, ki se pojavljajo na ta dan, povečal za faktor 1.0455. Za posameznega modela Poissonove je multiplikativni faktor vpliva je 1,0464, kar pomeni, da se za vsako povečanje minimalnega dnevnega atmosferskem tlaku za 1 enoto verjetnost dneva Biti GDV dan dobi pomnoži s faktorjem 1.0464. Upoštevajte, da je treba vse rezultate za zunanje kovariablo razlagati pogojno o tem, kaj se je zgodilo dva dni pred dnevom opazovanja. Tako je bolj natančno reči, da je verjetnost za GDV nastopu na kateri koli dan, povečal za faktor 1.0617 za vsako povečanje enote v minimalnega dnevnega atmosferskem tlaku, saj vemo, ali je bila ali ni šlo za GDV dva dni prej
. Zgornja izjava ne more biti, ne da bi vedel, kaj se je zgodilo dva dni pred dnevom opazovanja. To je pomembna razlika med našim pristopom in da redne modeliranja GLM, ali binarno GLM (logistični regresijski) ali modela Poissonov.
Razpravo in Zaključek
Prvič, izbranih je vsak od modelov, če pomembne informacije o morebitni etiološki dejavnik GDV in tako igra pomembno vlogo. To ni potrebno izbirati med njimi, če je edini namen je, da preuči možne pojasnjevalnih spremenljivk za GDV nastanka. Vendar pa to postane potrebno, če je napovedovanje prihodnjih GDV primerov glavni poudarek. Mi ne preverjamo to temo v trenutnem dokumentu.
Drugič, spremenljivke, opredeljene kot dejavniki bistveno vplivajo na stopnjo GDV pojava so bili minimalni dnevni pritisk na dan GDV, največji dnevni pritisk na dan GDV in Največji dnevni pritisk na dan pred dogodkom GDV. Minimalni dnevni pritisk na dan GDV bilo tudi ugotovljeno, da pomembna in statistično pomembnih dejavnikov v [7]. Znano je, da obstaja povezava med spremembami zračnim tlakom in nastopa dela pri ljudeh in SIDS (smrt sindrom nenadne dojenčkov) [11, 12]. Manj je znanega o povezavi med atmosferskim tlakom in udarci bolezni. Sedanja študija kaže, da lahko zračni tlak in spremembe v njej najbolj pomembni dejavniki, ki pojasnjujejo nastanek GDV pri psih.
Vrednost 2-dnevno odziv na lag pri modeliranju za je GDV nekoliko nepričakovano. Ta 2-dnevni rok ne nujno v korelaciji z 48-urnem obdobju med dogodke, vendar. Natančen začetek kaskadi dogodkov, ki vodijo do GDV je težko ugotoviti, zato lahko pride do patofiziološki dogodkov, ki vodijo do kliničnih znakov pri različnih hitrostih v različnih psov. Želodca napihnjenost je bilo ugotovljeno, da se hitro pojavljajo v nekaterih psih, in počasneje v drugih. Vloga spremenljivk, ki se lahko povežejo zamud v klinični manifestacije, kot tudi morebitna povezava (i) med vremenskih pojavov med takem časovnem oknu, bo še potrebno pojasniti.
Pristop z uporabo logistične model za binarne čas Zdi se, da je primeren, kadar obstajajo kvečjemu nekaj dnevnih opazovanj več kot 1 primeru GDV serije. Vendar to ne zgodi, če se ugotovi večja skupina psov in posledično število dni z več kot enim primeru GDV postane precejšen. Če se to zgodi, lahko Poisson GLM pristop je treba uporabiti izključno.
A zvezi papirja [8] uporablja latentno spremenljivko modeliranja, ki temelji na hierarhičnem pristopu BAYES vključiti odvisnost med pripomb. Ta pristop je nekoliko manj prilagodljiva kot pristop zagovarja v tem članku. Razlog za to je dejstvo, da je hierarhična Bayesov pristop zahteva nekatere posebne predhodne predpostavke, kot je normalno (ali druge posebne distribucije) podatkov, ki jih ni vedno lahko upraviči v praksi. Prav tako se zdi, da je subjektivna in ne temeljijo na posameznem izbirnem modela algoritem ker je ta raziskava ponuja vpogled v možne izbirnega postopka, ki temelji na merilih, kot AIC njihova izbira procesa, da 1 avtoregresivnega za latentne spremenljivke. Končno je treba tu opazili, da je serija pristop čas zelo naravno če obstaja vrsta opazovanj zabeleženih v daljšem časovnem obdobju. Če se to zgodi, se takšna opazovanja skoraj vedno povezana; ignoriranje te povezave lahko pride do izkrivljenega sklepanje o parametre interesa. Predvsem pa pogosto privede do pretirane ravni pomena za pojasnjevalnih spremenljivk. Zato je pristop časovno vrsto, ki temelji je, verjetno, ustrezno raziskovalno orodje v številnih kliničnih študijah, v katerih so bile pripombe, zabeleženih v določenem časovnem obdobju.
Metode
podatkov
GDV podatki pojav sklop je sestavljen iz vseh zabeležili primere GDV med vojaških delovnih psov (MWD) na Lackland Air Force Base (LAFB) od januarja 1993 do decembra 1998. v vsakem primeru je pasma prizadetega psa, njegovo spol, datum rojstva, starost ob nastopu bolezen in teža so bili zabeleženi. Vsi psi so bili eden od treh pasem: nemški ovčar, belgijski belgijski ovčar malinois ali nizozemski ovčar. Prvi zabeležen primer GDV nastopila Jan 6, 1993, zadnji pa na december 25, 1998. Skupno število zabeleženih primerov (tj dni, v katerih je bila registrirana GDV primer) je 60. Od 60, le dva dni vključeni več kot enem primeru GDV; za oba je bilo 2 prizadeti psi. Vse kenneled psi so preverili osebje vsake 3 ure na organizacijskih standardnimi postopki. Primeri so bili psi, ki dokazali v trebuhu oteklino, tympani v želodcu, in rentgenskimi znaki želodca dilatacijo kot veterinar določi. Kirurški poseg je bil začet na vseh primerih, bodisi zaradi smrtno nevarno stanje, ali za ne-nujnih primerih postopku profilaktično gastropexy.
Število psov na podlagi opazovanja na LAFB ni konstantna, temveč spreminja iz meseca v mesec. mesečni podatki popis Pes je bil na voljo oktober 1993 do december 1997 samo, začenši s 357 psi v oktobru 1993 in konča s 281 psom decembra 1997. Zaradi nedostopnosti popisnih podatkov za leto 1998, niso bili uporabljeni podatki o prisotnosti GDV za to leto.
velika baza vremenskih podatkov je sestavljen iz nacionalnega centra Climatic Data na Kelly Air Force Base, ki se nahaja neposredno ob LAFB. Vseboval urne podatke o smeri vetra, hitrost vetra sunek; urna temperatura v Fahrenheit stopinj, tako prilagoditi in neprilagojena za vlago in, končno, atmosferski tlak v centimetrov živega srebra, tako prilagojena na nadmorski in neprilagojene ena (v milibarov).
modeliranje pristop
Številni so bile upoštevane možne modele za nastanek GDV v populaciji psov. Pri vseh pa je bil pojav GDV na določen dan kodirana z 1 za GDV dan ali 0 za ne-GDV dan in se uporablja kot spremenljivke odziva. Druge količine, kot je, na primer, atmosferski tlak in temperaturo zraka, smo uporabili kot napovedovalec spremenljivk. Podatki binarni odziv bi lahko bilo več možnih pristopov, vključno z binarno GLM z logistično funkcijo povezave (logistični regresijski) in Poissonov GLM s funkcijo log povezave (Poisson regresijsko)
Tako odziv in spremenljivki smo zabeležili v daljšem časovnem obdobju.; zato je smiselno, da si ogledate tako odziv in Kovariable kot časovni vrsti. Zato namesto običajnih splošnega linearnega modela, da prevzame podatki so IID, smo izkoriščen modificirano obliko tega, kjer sta oba odziva in spremenljivki autocorrelated daljšem časovnem obdobju.
Poleg tega pristop časovne serije so koristne pri tej nastavitvi, ker je zelo verjetno je, da število (in morebitne druge) spremenljivki niso predstavljali, povezanih z vremenom; veliko število možnih etiološki dejavniki česar je precej težko vključiti vse od njih v enem modelu. Poleg temperature zraka in zračni tlak, ki je bilo obravnavano že prej, vlažnost zraka (bodisi absolutno ali relativno) je lahko eden od možnih etiološko dejavnikov. Vlažnost je zabeležena v daljšem časovnem obdobju in po navadi kaže opazno avtokorelacija. Značilno je, da je to misel kot časovne vrste; če je spremenljivka odziva resnično odvisna od vlažnosti, njena opustitev povzroča spremenljivko odzivnega posedovali časovno Autokorelacija. Ta linija razmišljanja kažejo, da je lahko serija model, tokrat v okviru GLM bolje opisati GDV pojav kot redni logističnega GLM model obravnava v [7]. Drugi spremenljivki, ki se običajno navedeni kot verjetne morebitne vzročne dejavnike GDV, kot so atmosferski tlak, temperatura zraka in drugih, so tudi naključni čas odvisni spremenljivki (časovne vrste) sami. Tako je opustitev kateri koli izmed njih
je verjetno, da povzroči dodatne avtokorelacije v odgovoru.
Iz več možnih pristopov modeliranja, te raziskave uporabljajo tisti, ki temelji na dajanje celo število vrednotijo časovne vrste v splošni linearni model okvir [13]. Za razliko od prejšnjega pristopa verige Markov, ne povzroča število parametrov, ki se ocenjuje, da eksponentno raste z velikostjo vzorca; je tudi dovolj široka, da zajame večino praktično pomembnih modelov. Upoštevajte, da niti Markov lastnina niti stacionarnost treba izhajati iz tega, ko zaposlujejo ta pristop. To je pomembno, ker lahko obe lastnosti težko preveriti v praksi. Nastale modeli se lahko oceni z uporabo iste metode (iterativno uteženi najmanjših kvadratov, IWLS na kratko) kot rednih splošnih linearnih modelov; edina razlika je, da so rezultati razlagati pogojno na preteklost.
GDV pojav na dan t
je bil označen kot Y
t
. Tako je Y
t
binarno. V spremenljivki lahko vključujejo pretekle in sedanje vrednosti pojasnjevalnih spremenljivk, kot tudi pretekle vrednote Y
t
. Vektor vseh spremenljivk je bil označen kot, kjer je p
število spremenljivk, k
število pojasnjevalnih spremenljivk zaostaja in q
števila preteklosti zaostankov y
t
šteje; za vsak 1 ≤ i
≤ p
in 1 ≤ j
≤ k
, ki jo zastopa, katerega vrednost i
th kovariablo v času t
- j
. Verjetnost primeru GDV na kateri koli dan je bil opredeljen kot p
t
ki je tudi funkcija kovariablo vektor vz
t
. Obstajata vsaj dva načina modeliranja verjetnosti GDV na določen dan. Prva izbira je, da uporabite binarni GLM s funkcijo logit zveza - učinkovito, a za model logistične regresije. Naključno del modela, potem je vektor binarnih vrednosti Y
t
ki so autocorrelated v daljšem časovnem obdobju. Sistematična komponenta, ki je posledica logističnega modela postane (1), kjer je α
razmak, β
je vektor koeficientov in p
t
je verjetnost dogodka GDV na določen dan t
, ki je odvisna od niza spremenljivk z t
. Za vsak GDV dan, je verjetnost dogodka opredeljena kot število primerov ugotovljene na ta dan, deljena s celotno populacijo psov, posnetih na ta dan. Ker so bili vsi GDV verjetnosti majhna v študiji, je tudi možno, da se model verjetnost dogodka GDV na določen dan t
uporabo Poissonove regresije. To pomeni, da je naključna komponenta modela vektor Y
t
ki so gledano sedaj kot šteje Poisson. Sistematična komponenta modela se nanaša na povprečno število zadev na dan t μ
t
na spremenljivk z uporabo dnevnika povezavo kot (2), če še enkrat, α
je razmak, β
je vektor koeficientov in μ
t
odvisna od niza spremenljivk z t
kot prej.
kot prvi korak v postopku izbire modela , dnevna značilnosti, kot max, min in pomeni, od tega so atmosferski temperatura tlak in zraka obravnavati kot morebitne spremenljivk. Temperatura ni bila prilagojena za vlago. Zapozneli vrednosti atmosferskega tlaka in /ali temperature lahko razumemo kot možne GDV vzročne dejavnike in s tem dodatnih pojasnjevalnih spremenljivk, kot dobro. Preskusi verjetnost, razmerje so bili uporabljeni za preverjanje statistično značilnost modela spremenljivk. Pojasnjevalne spremenljivke, ki so bile, ki se uporabljajo kot del zv izbrali so t
. Označimo minimalno dnevno atmosferski pritisk na določen dan pmin
t
, največji dnevni atmosferski tlak pmax
t
, največji dnevni ozračja temperatura tmax
t
in minimalna dnevna ozračja temperature tmin
t
. Pretekli vrednosti (na dan pred) iz zgoraj so pmin
t
-1, pmax
t
-1, tmax
t
-1 in tmint
t
-1. Največja urna dvig /padec atmosferskega tlaka na dan GDV dogodka je označen rp
t
in dp
t
, sicer pa je največja urna dvig /padec v temperaturi na dan GDV dogodka je označen rt
t
in dt
t
. pasma psov ni bila upoštevana, saj je bil pes prebivalstvo precej homogen, sestavljen iz treh velikih pasem rutinsko uporabljajo kot MWD. Vse dni brez dogodkov, so bile obravnavane v tej analizi, kot tudi.
Modeli so bili izdelani s pomočjo procesa postopno naprej izbire. V spremenljivki smo dodali zaporedoma in razmerje log-verjetnost za vsako novo sospremenljivko se izračuna. Da bi se izognili prezgodnjemu stop, čeprav hkratna ni dodali veliko opisnega sposobnost modela, merjeno po svoji log-verjetnost razmerje statistiko, postopek nadaljuje dokler se vse spremenljivk opisanih prej poskusili. Število zamikov y
t
vključeni v obravnavanih modelov v tej raziskavi je bil omejen na 3, da bi zagotovili parsimoniousness modelov. Na ostanke vsakega modela, ki ga kasneje lahko analizirajo vzorce avtokorelacije in dodal dodatnih zamikov, če je to potrebno. Koeficienti Y
t
-1 in Y
t
-3 je zelo velik koeficient log-verjetnost p-vrednosti, ne glede na to, ki so bili vključeni zunanji spremenljivki v modelu; natančneje, njihove log-verjetnost razmerje p-vrednost presega 0,1 povsod in tako so bili izključeni iz končnih modelov.
modeli izbrane kot finala so prikazani v tabeli (1). Razen najnižje atmosferskega pritiska na GDV dan in maksimalno atmosferskem tlaku na dan GDV dogodka in na dan pred dogodkom GDV, vseh drugih zunanjih spremenljivk prikaz log vjerojatnošću razmerje p-vrednosti nad izbrano mejno vrednostjo 0,10 sta niso vključeni.
Vsi modeli iz preglednice (1) so sposobne pomočjo iterativnega uteženi najmanjših kvadratov algoritem pogosto uporablja za vgradnjo splošnih linearnih modelov. Glede na to, da smo z kanonično funkcijo povezava dnevnik binarnih podatkov, nepravilnega uteženi najmanjših kvadratov algoritem sovpada z rednim Newton-Raphsonovo algoritem v tem primeru.
Deklaracijah
Zahvala
Avtorji zahvalil veterinarji Ministrstvo za obrambo vojaške delovne pse veterinarski službi, ki je milostno je zagotovil nabor podatkov in poskušala zmanjšati pojavnost GDV v vseh psih. Prav tako bi se rad zahvalil prof Bruce Craig iz oddelka za statistiko na univerzi Purdue, s katerimi je imel avtor številne koristne razprave in iz katerega pomoč obema koristile. Originalne predložene datoteke
avtorjev za slike
Spodaj povezave do izvirniku avtorjev prenosov datotek za slike. "Izvirno datoteko na sliki 1 12917_2008_146_MOESM2_ESM.eps avtorjev 12917_2008_146_MOESM1_ESM.eps avtorjev prvotne datoteke za izvirno datoteko številka 2 12917_2008_146_MOESM3_ESM.eps avtorjev po sliki 3
 PENTAX Medical zbere 125 USD,
PENTAX Medical zbere 125 USD,
 Ulcerozni kolitis
Ulcerozni kolitis
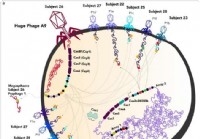 Na novo odkriti veliki fagi zamegljujejo življenjsko/neživljenjsko mejo
Na novo odkriti veliki fagi zamegljujejo življenjsko/neživljenjsko mejo
 Formula na osnovi kozjega mleka je dobra za zdravje črevesja dojenčkov
Formula na osnovi kozjega mleka je dobra za zdravje črevesja dojenčkov
 Mikrobiom bi lahko pomagal pri prepoznavanju tveganja pred rakom pri ženskah s HPV
Mikrobiom bi lahko pomagal pri prepoznavanju tveganja pred rakom pri ženskah s HPV
 Nekatere črevesne bakterije lahko povečajo tveganje za raka na črevesju
Nekatere črevesne bakterije lahko povečajo tveganje za raka na črevesju
 Glicirizinska kislina kot kandidat za zdravilo za COVID-19
Terapevtov za preprečevanje škode, ki jo povzroči hudi akutni respiratorni sindrom koronavirus 2 (SARS-CoV-2), je bilo malo in daleč, kljub prizadevanjem za odkrivanje novih zdravil in ponovno uporabo
Glicirizinska kislina kot kandidat za zdravilo za COVID-19
Terapevtov za preprečevanje škode, ki jo povzroči hudi akutni respiratorni sindrom koronavirus 2 (SARS-CoV-2), je bilo malo in daleč, kljub prizadevanjem za odkrivanje novih zdravil in ponovno uporabo
 Ali oznake na komercialnih izdelkih s kefirjem pravilno poročajo o mikrobni ravni?
Črevesni mikrobiom je bistveni del človeškega organizma, kot je postalo povsem jasno iz številnih raziskav, opravljenih v zadnjih nekaj desetletjih. Mednarodno znanstveno združenje za probiotike in pr
Ali oznake na komercialnih izdelkih s kefirjem pravilno poročajo o mikrobni ravni?
Črevesni mikrobiom je bistveni del človeškega organizma, kot je postalo povsem jasno iz številnih raziskav, opravljenih v zadnjih nekaj desetletjih. Mednarodno znanstveno združenje za probiotike in pr
 Zaporedje RNA ponuja nov vpogled v mikrobiom
Raziskovalci na Univerzi v Chicagu so pripravili revolucionarno strategijo za preučevanje aktivnosti črevesnega mikrobioma-z uporabo visoko zmogljivega zaporedja tRNA. 3D grafika Alpha Ta
Zaporedje RNA ponuja nov vpogled v mikrobiom
Raziskovalci na Univerzi v Chicagu so pripravili revolucionarno strategijo za preučevanje aktivnosti črevesnega mikrobioma-z uporabo visoko zmogljivega zaporedja tRNA. 3D grafika Alpha Ta