vremenske serije modela nastanka želučanog dilatacijskog-volvulus u populaciji pasa
Sažetak
Pozadina
želučani dilatacijskog-volvulus ( GDV) je po život opasno stanje sisavaca, s povećanim rizikom u velikim pasmina pasa. Studija njegovih etioloških čimbenika je teško zbog raznih mogućih životnih uvjeta. Veza između meteoroloških zbivanja i pojave GDV je pretpostavio, ali ostaje nejasno. Ova studija predstavlja binarnu vremenske serije pristup istraživanju mogućih meteoroloških faktora rizika za GDV. Podaci prikupljeni u populaciji od visokog rizika radnih pasa u Teksasu je korištena. | Rezultati
minimalni i maksimalni dnevni atmosferski tlak na dan GDV događaja i maksimalne dnevne atmosferskog tlaka na dan prije GDV događaja bili su pozitivno povezan s vjerojatnošću GDV. Svi su izgledi /višestruke čimbenike jednog dana bude GDV dan interpretirane su uvjetno na proteklih GDV pojava. Bilo je minimalna razlika između binarnih i Poissonov općeg linearnog modela. Pregled Zaključak pregled vremenskih serija modeliranje pruža novi postupak za ocjenu povezanost između meteoroloških varijabli i GDV u velikoj populaciji pasa. Odgovarajuća primjena ove metode je pojačana zajedničkom okolišu za pse i dostupnost meteoroloških podataka. Potencijal interakcija između vremenskih promjena i faktorima rizika pacijenta za GDV zaslužuje daljnje istraživanje. Pregled Pozadina pregled želuca dilatacija-volvulus (GDV) je stanje u kojem se želudac proširuje i rotira na sebe, što dovodi postupno do hipotenzije, šoka, i smrt. Veliki pasmina pasa često su pogođeni, iako to može utjecati na mnoge životinjske vrste, uključujući čovjeka [1].
Fizičke mehanizme uključene u ovom stanju i njenom liječenju su dobro poznati, ali uzroci nisu [2]. Uzroci GDV može se smatrati predisponirajući (čime se povećava vjerojatnost oboljenja) ili taloženjem (pokreće nastanak bolesti). Nekoliko prijemljivih faktori rizika kod pasa su predložene, uključujući i temperament psa (razdražljivost), velike ili divovske pasmine, povećana prsne dubinu omjeru širine i brzog konzumiranja hrane [2-4]. Međutim, mnoga pitanja vezana za stvarne početka ove opasne po život bolest ostaje neobjašnjena od tih faktora rizika.
Proučavanje taloženjem uzroke GDV je važan, a ne vrlo dobro istražena područja. U mnogim slučajevima GDV, želudac rasteže s plinom; Među mogućim izvorima ovog plina, aerophagia, fermentacija-truljenje, kemijska plin postanak i difuzija plina su predložene. To je, zajedno s promatranom sezonske varijacije u GDV slučajevima dovela je do sumnje o mogućoj povezanosti između GDV i vremenskih uvjeta neposredno prije njegove pojave [5, 6]. Metoda koje Herbold i sur, u [5], to jest osnovne komponente analize, odaberite eventualno važni Klimatološka faktori mogu imati zasjenio utjecaj jednog vremena vezane varijable. Druge studije su koristili logističke regresije da istraže vjerojatnost jedan dan, koja je GDV dan, s obzirom na određeni atmosferski tlak ili temperaturnim uvjetima [6, 7]. Takvi pristupi temelje se na pretpostavci da GDV događaji su međusobno neovisni i ne postoji jaka korelacija između događaja tijekom vremena, kao što bi se dogoditi ako se bolest su zarazne. Međutim, kao što je zapravo, većina meteoroloških kovarijable mislili da utječu GDV pojavu su autokorelaciju tijekom vremena i treba biti misao kao vremenske serije. Ako neki od njih nisu bili uključeni u potencijalni model, ali oni ne utječu na GDV pojavu, GDV incidencija zabilježena tijekom vremena može biti u korelaciji. Pregled Dakle, gledanje podatke GDV pojava što su vremenske serije svibanj biti poželjno u praksi. Iako tradicionalno vremenske serije modeliranje ima ograničenu primjenjivost u proučavanju neobičnih bolesti, nedavno je koristiti za dokazivanje sezonsku komponentu drugoj bolesti probavnog sustava, naime, kolike u konja [8]. Budući da je pojava podaci GDV jasno vrijednost cijelog broja (vrijednost odgovor je broj GDV slučajeva dnevno), više tradicionalne metode vremenskih serija, poput onih koje se koriste u klasičnom autoregresijski Integrirani pomični prosjek (ARIMA) okvir [9] ne mogu se koristiti. Jedan od ranijih referenci [8] sugerira da «... jedna mogućnost je u upotrebi Poisson-ovoj razdiobi kao model podataka računati u okviru široko analogan onom generaliziranog linearnog modela ..."; ovaj prijedlog učinkovito iznosi primjenom pristupa na temelju generaliziranog linearnog modela (GLM) okvira koji se koristi u ovom rukopisu.
Cilj ovog istraživanja bio je koristiti vremenski serije pristup istražiti povezanost između meteoroloških varijabli i GDV pojave u pasa. Da bi se smanjila varijabilnost predisponirajući čimbenici rizika i konfuznih varijable kao što su prehrana i stambenog okoliša [2], ako je skup velikih pasmina pasa smještenih u radni pas vojnog (MWD) Training Center u bez zemlje Air Force Base (LAFB) se koristi. U ovom zajedničkom okruženju, psi su hranjeni standardnu dijetu, smješten u otvorenom staze, a nalaze se na promatranju 24 sata dnevno. Ovaj set podataka je prije korišteni u logističke regresije pristup istraživanju meteorološke varijable i GDV [7], a usporedba metodoloških pristupa, dakle, može također biti. Pregled Rezultati
nekoliko modela koji su imali neke od najniže vrijednosti od AIC (Akaike Information Kriterij) prikazani su u tablici 1. za svaku od njih, sustavno dio se daje zajedno s tipu modela (binarni GLM ili Poisson GLM) i vrijednostima AIC. Samo modeli koji su imali log-vjerojatnost omjer p-vrijednosti svih kovarijanata ispod 0.10 bio uključen. Budući da je popis stanovništva psa varira od dana do dana, iznos izloženosti danas je promjenjiva. To može učiniti strogo Poissonova /binarni pretpostavku o podacima nerealnim. U slučaju Poissonovog, to znači da je odstupanje ne mora biti točno jednako srednje vrijednosti. U binarnom slučaju, varijanca ne može biti točno jednaka varijance Bernoullijeva razdiobe za dani skup kovarijan vrijednosti. Dakle, čini se razumnim za provjeru mogućeg overdispersion u podacima. Jednostavan kvazi-vjerojatnost pristup korišten je u potrazi za dokazima o overdispersion [10]. Procijenjena koeficijent je uvijek blizu 1 i na taj način ne postoji ne čini da se svaki ozbiljan dokaz overdispersion u ovom setting.Table 1 konačnog modela pregled
Model
pregled sustavnim dijelom
Vrsta modela
AIC
Overdispersion faktor
1 pregled β pregled 0 + β
1Y pregled t pregled -2 + β pregled 2pmin pregled t
Binary GLM
411,02 pregled 1,02 pregled 2 pregled, β pregled 0 + β pregled 1Y pregled t pregled -2 + β pregled 2pmin pregled t
Poisson GLM
407,92 pregled 0,98 pregled 3 pregled β
0 + β pregled 1Y pregled t pregled -2 + β pregled 2pmax pregled t pregled -1 pregled Binarni GLM
406,47 pregled 1 pregled 4 pregled β pregled 0 + β pregled 1Y pregled t pregled -2 + β pregled 2pmax pregled t pregled -1 pregled Poisson GLM
403,42 pregled 0.95 pregled 5
β
0 + β pregled 1Y pregled t pregled -2 + β pregled 2pmax pregled t
Binary GLM
410.46
1,02 pregled 6
β
0 + β pregled 1Y pregled t pregled -2 + β pregled 2pmax pregled t
Poisson GLM
407,40 pregled 0,97 pregled Ispitivanje zaostalih autokorelacije parcelama pokazuje da su radni ostataka autokorelacije zemljišta gotovo su istovjetne, a sve od njih nije pokazao značajan preostali autokorelacije. Na temelju toga, ove tri modela pojavljuju pružiti adekvatnu stane za GDV pojava podaci Y Netlogu
t pregled.
Koeficijenti u tim modelima su tumačiti kao bilo log izgleda (OR) u binarnom GLM modeli ili multiplikativnih čimbenici (MF) u Poisson GLM modelima. Tablica 2 sadrži vrijednosti omjere i multiplikativnom čimbenike za zaostaje odziva Y Netlogu t pregled -2 i vanjski kovarijan za sve modele iz tablice 1. Ona također sadrži i logaritamske vjerojatnosti p-vrijednosti za sve omjera šansi. U imenima stupaca tablice 2, ili stajati za omjer vjerojatnosti i MF za multiplikativni faktor; "druga kovarijan ILI" je ili minimalna dnevna atmosferski pritisak na GDV dana Pmin pregled t pregled, maksimalna dnevna atmosferski tlak na GDV dana Pmax pregled t pregled ili maksimalno svakodnevno atmosferski pritisak na dan prije GDV dana Pmax pregled t pregled -1. LL stoji za log-vjerojatnost. Budući da je vjerojatnost GDV događaja na bilo koji dan je mala i vrijednosti popisa psa su u stotinama, model može biti u formi ili kao binarni GLM ili Poisson GLM. Oba pristupa su zaposleni za usporedbu. Bilo je vrlo malo razlika između binarnog GLM i Poisson GLM u slučaju za sve skupove kovarijanata considered.Table Izbor 2 Model pregled Model pregled
ILI Y pregled t pregled -2
LL p-vrijednost
Ostalo kovarijan ILI /MF
LL p-value
1
3.1606
0.0595
1.0455
0.0891
2
3.0862
0.0640
1.0464
0.0833
3
2.9492
0.0741
1.0663
0.0064
4
2.8711
0.0807
1.0664
0.0062
5
3.0198
0.0693
1.0456
0.0633
6
2.9498
0.0741
1.0460
0.0606
Among konačna grupa modela prikazanih bilo nikoga tko smatra vanjske kovarijable na odmakom od više od 1 dana. Takvi modeli su smatrani tijekom faze odabira modela, no. U svim tim slučajevima, omjer log-vjerojatnost p-vrijednost vanjskog kovarijata zaostaje više od 1 dana bio je znatno iznad 0,10, dok je koeficijent za dva dana odmakom od odgovora Y pregled t
-2 imao omjer log-vjerojatnost p-vrijednost stalno ispod 0,10. Dakle, izbor kovarijanata nije pristran u korist pomaka od odgovora Y Netlogu t pregled na teret vanjskog kovarijata zaostaje.
Temelju tih modela, čini se da su faktori koji utjecati na stopu GDV najviše primjetno stoga je minimalna dnevna atmosferski tlak na dan GDV događaja, najvećim dnevnim atmosferskog tlaka na dan GDV događaja i maksimalne dnevne atmosferskog tlaka na dan prije GDV događaja. U omjeri /multiplikativnih faktori vanjskog kovarijata na svim modelima su nešto veći od 1 što ukazuje na pozitivnu povezanost između tih faktora i vjerojatnosti GDV događaja na određeni dan. Na primjer, minimalna dnevna atmosferski tlak na dan GDV slučaju ima izgledi omjer 1.0455 za binarni GLM modelu. To znači da za svaki povećanja minimalne dnevne atmosferskog tlaka za 1 jedinicu, izgledi slučaju GDV se dogodila na taj dan povećao za faktor od 1.0455. Za dotičnog Poissonovog modelu, multiplikativni faktor utjecaja je 1,0464 što znači da je za svaku povećanja minimalne dnevne atmosferskog tlaka za 1 jedinicu vjerojatnost dana a koji je GDV dan dobiva množi s faktorom 1.0464. Imajte na umu da sve rezultate za vanjsku kovarijata treba tumačiti uvjetno na ono što se dogodilo dva dana prije dana promatranja. Dakle, to je točnije reći da su izgledi GDV pojave na bilo koji dan povećao za faktor od 1.0617 za svako povećanje udjela minimalne dnevne atmosferskog tlaka s obzirom da znamo da li postoji ili ne bio slučaj GDV dva dana ranije pregled. Navedena izjava ne može biti ne znajući što se dogodilo dva dana prije dana promatranja. To je važna razlika između našeg pristupa i onom regularnom GLM modeliranje, bilo binarnog GLM (logistička regresija) ili Poisson model. Pregled Rasprava i zaključak
Prvo, svaki od modela odabrane daje važne informacije o mogućim etiološki faktor GDV i prema tome ima korisnu ulogu. Nije potrebno napraviti izbor između njih, ako je jedina svrha je da pogledate u mogućim objašnjenjima kovarijanata za GDV pojave. Međutim, to postaje nužno ako je predviđanje budućih GDV incidencija je glavni fokus. Mi ne istražiti tu temu u ovom radu.
Drugo, varijable identificirani kao čimbenici značajno utječu na stopu GDV pojave su minimalni dnevni pritisak na dan GDV, maksimalne dnevne pritiska na dan GDV i maksimalna dnevna pritisak na dan prije GDV događaja. Minimalna dnevna pritisak na dan GDV je također identificiran kao važan i statistički značajnih čimbenika u [7]. Poznato je da postoji veza između promjene barometarskog tlaka i početka rada kod ljudi i SIDS (sindrom iznenadne smrti djeteta) [11, 12]. Manje se zna o povezanosti između atmosferskog tlaka i pseće bolesti. Trenutna studija sugerira da je atmosferski tlak i promjene u njemu mogu biti najvažniji čimbenici objašnjavaju nastanak GDV u pasa.
Vrijednost 2 dana kašnjenja odgovora u modeliranju za GDV je nešto neočekivano. Ovaj 2-dnevno razdoblje ne moraju nužno korelirati periodu od 48 sata između događaja, no. Točan početak kaskada događaja koji vode do GDV je teško utvrditi, i patofiziološki događajima koji su doveli do kliničkih znakova mogu se pojaviti pri različitim brzinama u različitim psima. Želučani rastezanje je napomenuti da se javljaju vrlo brzo u nekim psima, a sporije u drugima. Uloga kovarijanata koja bi mogla biti povezana s kašnjenjem u kliničkoj manifestaciji, kao i mogući odnos (e) između meteoroloških pojava pri takvom prozor vremena, tek treba razjasniti.
Pristup pomoću logističkog modela za binarni vrijeme serija Čini se da je odgovarajuća u slučaju gdje postoje najviše nekoliko dnevnih opažanja sa više od 1 GDV slučaju. Međutim, to ne mora biti slučaj ako je uočena veća skupina pasa i, kao posljedica toga, broj dana s više od jednog slučaju GDV postaje poveliki. Ako se to dogodi, Poissonova GLM pristup može se moraju koristiti isključivo.
Papirnatom vezane [8] koristi latentnu varijablu modeliranje temelji na hijerarhijskoj Bayes pristupa ugraditi ovisnost između opažanja. Ovaj pristup je nešto manje fleksibilan od pristupa zagovara u ovom radu. Razlog tome je činjenica da je hijerarhijski Bayesov pristup zahtijeva određene specifične prethodne pretpostavke, poput normalnog (ili neke druge specifične distribucije) podataka, koji nisu uvijek lako opravdati u praksi. Također, njihov izbor autoregresijski procesa za latentne varijable kako bi 1. Čini se da je subjektivno, a ne na temelju bilo kojeg algoritma odabira modela, a ovo istraživanje pruža uvid u mogući mehanizam selekcije na temelju kriterija kao što su AIC. Konačno, važno je primijetiti da se ovdje serije pristup je vrlo prirodno kada postoji niz promatranja zabilježene tijekom vremena. Ako se to dogodi, takve primjedbe su gotovo uvijek u korelaciji; ignoriranje ovu povezanost može rezultirati iskrivljenom zaključak u pogledu parametara od interesa. Konkretno, to često rezultira pretjeranim razinama od značaja za nezavisne varijable. Dakle, pristup vremenske serije temelji se, vjerojatno, odgovarajući istraživački alat u mnogim kliničkim studijama u kojima su zapažanja su zabilježene tijekom određenog vremenskog razdoblja.
Metode pregled podataka
GDV skup pojava podataka sastoji se od svega zabilježila slučajeve GDV među vojnim rade pasa (MWO) na bez zemlje Air Force Base (LAFB) od siječnja 1993. do prosinca 1998. u svakom slučaju, pasmina zahvaćena psa, njegova spola, datuma rođenja, godine života na samom početku bolest i težina su snimljeni. Svi psi bili su jedan od tri pasmine: njemački ovčar, belgijski Malinois ili nizozemski pastir. Prvi zabilježeni slučaj GDV dogodio Jan 6, 1993 i posljednjeg dana pro 25, 1998. Ukupan broj zabilježenih slučajeva (tj dane u kojima je zabilježen GDV slučaj) je 60. Od 60 godina, samo dva dana su uključeni više od jedne slučaju GDV; na njih oboje, bilo je 2 pogođene psi. Svi kenneled psi su provjereni od strane osoblja svaka 3 sata po organizacijskim standardnim postupcima. Slučajevi su psi koji su pokazivali u trbuhu oteklina, zabatima želuca i radiografski dokaz želučanog dilatacije kako je određeno od strane veterinara. Kirurška intervencija je pokrenuta na svim slučajevima, bilo zbog po život opasno stanje ili ne-hitne procedure profilaktičko gastropexy.
Broj pasa na promatranju u LAFB nije bila konstantna, već se mijenjaju iz mjeseca u mjesec. mjesečni podaci za popis pas bio dostupan listopada 1993 do prosinca 1997. godine samo, počevši od 357 pasa u listopadu 1993. godine, a završava s 281 pasa u prosincu 1997. Zbog nedostupnosti podataka o broju stanovnika za 1998. godinu, GDV pojave podaci za tu godinu nisu bili korišteni.
velika baza podataka o meteorološkim podacima je sastavljen iz Nacionalnog centra za klimatske podatke na Kelly Air Force Base, koji se nalazi neposredno uz LAFB. Ona sadrži satu podatke o smjeru vjetra, brzine i vjetra nalet; satu temperatura u celzijusa stupnjeva, kako podesiti i neusklađeno za vlažnost i, konačno, atmosferski tlak u inčima žive, i prilagoditi razine mora, a nekorigirani jedan (u milibara). pregled Modeliranje pristup
A broj smatrani su mogući modeli za GDV pojave u psa stanovništva. U svima njima, pojava GDV na zadani dan je kodiran pomoću jedne za GDV dan ili 0 za ne-GDV dan u i koristi se kao varijabla odgovora. Druge količine, kao što je, na primjer, atmosferski tlak i temperature zraka, korišteni su kao prediktorskih varijabli. Podaci binarni odgovor pada u broju mogućih pristupa, uključujući binarnom GLM u funkciji logističkih veza (logistička regresija) i Poisson GLM s funkcijom dnevnika veza (Poissonova regresije) pregled Oba odgovora i kovarijable su zabilježene tijekom vremena. to ga čini razumno pogledati oba odgovora i kovarijable kao vremenske serije. Dakle, umjesto uobičajenog generaliziranog linearnog modela koji pretpostavlja podaci su jednako distribuirane, mi korištena je modificirana forma tome u kojem su oba odgovora i kovarijable autokorelaciju tijekom vremena.
Osim toga, u vrijeme serije pristup je koristan u ovom okruženju, jer je vrlo vjerojatno da je jedan broj vremenskih povezanih (i eventualno druge) kovarijable nisu činili; veliki broj mogućih etioloških čimbenika čini vrlo teško uključiti sve od njih u jednom modelu. Osim temperature zraka i atmosferskog tlaka koji su smatrani ranije, vlažnosti zraka (apsolutne ili relativne) može biti jedan od mogućih etioloških čimbenika. Vlaga se bilježi tijekom vremena i obično pokazuje zamjetnu autokorelacije. Tipično, to se misli kao vremenske serije; ako je varijabla odgovora je uistinu ovisi o vlažnosti zraka, njegov propust uzrokuje varijablu odgovora pokazuju privremeni autokorelacije. Ova linija razmišljanja sugerira da je vrijeme modela serije u GLM okviru može biti bolje opisati GDV pojavu od redovne logističku GLM modelu smatraju u [7]. Ostali kovarijable koji se najčešće navode kao vjerojatne mogućih etioloških čimbenika GDV, poput atmosferskog tlaka, temperature zraka i drugih, također su slučajni vremenski ovisne kovarijable (vremenskih serija) sami. Dakle, izostavljanje bilo kojeg od njih pregled je vjerojatno da će izazvati dodatni autokorelacije u odgovoru.
Od nekoliko mogućih pristupa modeliranju, ovo istraživanje koristi onaj koji se temelji na stavljanje cjelobrojne vrijednosti vremenske serije u generaliziranog linearnog Model okvir [13]. Za razliku od ranijih lanca pristupa Markov, to ne uzrokuje broj parametara koji se procjenjuju da raste eksponencijalno s veličinom uzorka; to je dovoljno širok da obuhvati većina praktično važne modele. Imajte na umu da ni Markov svojstva ili stacionarnost moraju se pretpostaviti kada se koristi ovaj pristup. To je važno jer oba ova svojstva mogu biti teško provjeriti u praksi. Nastale modeli mogu se procijeniti korištenjem iste metode (iterativni reweighted najmanjih kvadrata, IWLS skraćeno) kao redovne generaliziranog linearnog modela; jedina razlika je u tome što su rezultati moraju se tumačiti uvjetno na prošlost.
GDV pojavu na dan t Netlogu bio označen kao y pregled t
. Dakle, y pregled t pregled je binarno. U kovarijable mogu uključivati prošlosti i sadašnjosti vrijednosti nezavisne varijable, kao i prošle vrijednosti od Y pregled t
. Vektor svih kovarijanata se označava kao gdje je p pregled je broj kovarijanata, k pregled broja nezavisnih varijabli zaostaje i q pregled broja prošlosti zaostaje od Y pregled t
uzeti u obzir; za svako 1 ≤ i ≤ P
i 1 ≤ j ≤ k pregled pregled, koju zastupa vrijednosti i
th kovarijan u vremenu t pregled - j
. Vjerojatnost GDV slučaju na bilo koji dan bila definirana kao p Netlogu t pregled koji je također funkcija kovarijan vektor z pregled t pregled. Postoje najmanje dva moguća načina modeliranja vjerojatnosti GDV na određeni dan. Prvi izbor je koristiti binarni Glm s funkcijom logit veze - učinkovito, logističke regresije. Slučajan komponenta modela tada je vektor binarnih vrijednosti Y Netlogu t pregled koji se autokorelaciju tijekom vremena. Sustavno dio dobivenog logističkog modela postaje (1) gdje je α pregled je presresti, β pregled je vektor koeficijenata i p Netlogu t pregled je vjerojatnost GDV događaja na dano dan t pregled koji ovisi o nizu kovarijanata z t pregled. Za svaki GDV dan, vjerojatnost događaja je definiran kao broj zabilježenih slučajeva tog dana podijeljena s ukupnom populacijom pasa snimljenih na taj dan. Zbog svega GDV vjerojatnosti su male u studiju, također je moguće modelirati vjerojatnost GDV događaja na određeni dan t pregled pomoću Poissonov regresiju. To znači da je slučajna komponenta modela je vektor Y Netlogu t pregled da se gleda sada kao Poissonov broji. Sustavno komponenta modela odnosi se na prosječan broj predmeta na dan t μ pregled t pregled na kovarijanata pomoću zapisnika vezu kao (2) gdje je, opet, α pregled je presresti, β pregled je vektor koeficijenata i μ pregled t pregled ovisi o skupu kovarijanata z t pregled kao i prije.
kao prvi korak u postupku odabira modela , dnevne karakteristike, kao što su max, min i mislim, od temperatura atmosferski tlak i zrak su se smatrali mogućim kovarijanata. Temperatura ne podesi na vlagu. U zaostaje vrijednosti atmosferskog tlaka i /ili temperature može se promatrati kao mogući GDV etioloških čimbenika i na taj način dodatne nezavisne varijable, kao dobro. Vjerojatnost omjer testovi su korišteni za provjeru statističke značajnosti modela kovarijanata. Objašnjenja varijable koje će se koristiti kao dio z t pregled su izabrani. Neka nam označavaju minimalni dnevni atmosferski tlak na zadani dan Pmin pregled t pregled, maksimalna dnevna atmosferski tlak Pmax pregled t pregled, maksimalna dnevna atmosferska temperatura tmax pregled t pregled, a minimalna dnevna atmosferska temperatura tmin pregled t pregled. Prošli vrijednosti (na dan prije) gore su Pmin pregled t pregled -1, Pmax pregled t pregled -1, tmax pregled t pregled -1 i tmint pregled t pregled -1. Maksimalna satu porast /pad atmosferskog tlaka na dan GDV događaj je označen RP
t pregled i DP pregled t pregled, odnosno dok je maksimalna satna porast /pad u temperaturi na dan GDV događaj je označen rt pregled t pregled i dt pregled t pregled. pasmina za pse ne smatra jer je pas stanovništvo je prilično homogena se sastoji od tri velike pasmine rutinski koriste kao MWD. Svi dani bez događaja su razmatrani u ovoj analizi, kao dobro.
Modeli su konstruirani pomoću procesa postupne naprijed selekcije. U kovarijable, sukcesivno, a omjer log-vjerojatnost za svaku novu kovarijata izračunava. Kako bi se izbjeglo prerano zaustavljanje, čak i ako je kovarijan nije dodao mnogo opisnom sposobnosti modela, mjereno po log-vjerojatnost omjer statistike, proces nastavlja sve dok svi kovarijanata ranije opisane su pokušali. Broj pomaka od Y pregled t pregled uključen u modelima smatraju u ovom istraživanju bio je ograničen na 3 kako bi se zajamčilo parsimoniousness od modela. Ostataka za svaki model i naknadno može biti analiziran autokorelacije uzoraka i dodaje se dodatna zaostaje, ako je potrebno. Koeficijenti y pregled t pregled -1 i Y pregled t pregled -3 je vrlo velik omjer log-vjerojatnost p-vrijednosti, bez obzira na koji vanjski kovarijable su uključene u model; točnije, njihovi log-Vjerojatnost omjer p-vrijednosti premašuje 0,1 svugdje i na taj način bili su isključeni iz konačnih modela.
modela izabrana kao finale prikazani su u tablici (1). Osim minimalnog atmosferskog tlaka na GDV dan i maksimalnim atmosferskog tlaka na dan GDV događaja i na dan prije GDV slučaju, sve ostale vanjske kovarijanata prikazati log-vjerojatnost omjer p-vrijednosti iznad odabranog praga od 0,10 su nije uključen.
Svi modeli koji se nalaze u tablici (1) u formi pomoću iterativnog reweighted najmanjih kvadrata algoritam obično koristi za ugradnju generaliziranih linearnih modela. S obzirom da smo koristeći kanonski Link funkciju dnevnika za binarne podatke, iterativni reweighted najmanjih kvadrata algoritam podudara s redovitim Newton-Raphson algoritma u ovom slučaju. Pregled deklaracija
Zahvale pregled Autori zahvaliti veterinari iz Ministarstvo obrane Vojne radni pas veterinarske službe, koji je ljubazno pruža niz podataka i nastoje smanjiti učestalost GDV u svim psima. Također želimo zahvaliti prof Bruce Craig iz Odjela za statistiku na Purdue University s kojima su autori imali niz korisnih rasprava i od čije pomoći i od njih koristi.
Autora originalne dostavljeni datoteke za slike
Slijedi linkovi na originalu autora poslanih datoteka za slike. Izvorna datoteka za sliku 1 12917_2008_146_MOESM2_ESM.eps autorskim 12917_2008_146_MOESM1_ESM.eps autora izvorne datoteke za sliku 2 12917_2008_146_MOESM3_ESM.eps autorskim izvorne datoteke za slike 3
 Neil Bell imenovan je za glavnog direktora razvoja Avacta Life Sciences
Neil Bell imenovan je za glavnog direktora razvoja Avacta Life Sciences
 Krvni test za mikrobnu DNK mogao bi upozoriti na rak
Krvni test za mikrobnu DNK mogao bi upozoriti na rak
 Veliko istraživanje pokazalo je da je SARS-CoV-2 virusno opterećenje najniže u djece
Veliko istraživanje pokazalo je da je SARS-CoV-2 virusno opterećenje najniže u djece
 Označavanje potencijalnih molekularnih prediktora odgovora na biološke terapije u ulceroznom kolitisu
Označavanje potencijalnih molekularnih prediktora odgovora na biološke terapije u ulceroznom kolitisu
 Crijevne bakterije povezane s metaboličkim promjenama i autizmom u novoj studiji
Crijevne bakterije povezane s metaboličkim promjenama i autizmom u novoj studiji
 Dobre vijesti za oboljele od IBS -a jer istraživači identificiraju "svrbež u crijevima"
Dobre vijesti za oboljele od IBS -a jer istraživači identificiraju "svrbež u crijevima"
 Mikrobiomi spermija otkriveni sekvenciranjem RNA
Nova studija izvještava o prvom detaljnijem opisu mikrobioma ljudske sperme, korištenjem novijih tehnika sekvenciranja RNA koje mogu razlikovati RNK sperme od one bakterijske kontaminacije ili koloniz
Mikrobiomi spermija otkriveni sekvenciranjem RNA
Nova studija izvještava o prvom detaljnijem opisu mikrobioma ljudske sperme, korištenjem novijih tehnika sekvenciranja RNA koje mogu razlikovati RNK sperme od one bakterijske kontaminacije ili koloniz
 Bakterije u rodnom kanalu povezane su s manjim rizikom od raka jajnika
Nova studija pokazuje da nešto tako jednostavno kao što je bris cerviksa može imati potencijal pomoći stotinama žena koje su u iznimno velikom riziku od raka jajnika jer imaju mutaciju u genu BRCA1.
Bakterije u rodnom kanalu povezane su s manjim rizikom od raka jajnika
Nova studija pokazuje da nešto tako jednostavno kao što je bris cerviksa može imati potencijal pomoći stotinama žena koje su u iznimno velikom riziku od raka jajnika jer imaju mutaciju u genu BRCA1.
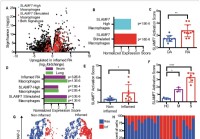 Novi super aktivirajući receptor makrofaga mogao bi objasniti hiperinflamaciju u teškom obliku COVID-19
Imunitet je zanimljiva stvar. Iako je bitan u zaštiti tijela od invazije patogena i stranih antigena, također se može okrenuti protiv tijela i pokrenuti destruktivne imunološke procese. Nova studija o
Novi super aktivirajući receptor makrofaga mogao bi objasniti hiperinflamaciju u teškom obliku COVID-19
Imunitet je zanimljiva stvar. Iako je bitan u zaštiti tijela od invazije patogena i stranih antigena, također se može okrenuti protiv tijela i pokrenuti destruktivne imunološke procese. Nova studija o