Az idősor modell előfordulásának gyomor dilatáció-volvulus populációját kutyák katalógusa Abstract Background katalógusa katalógusa Gyomor dilatáció-volvulus ( GDV) egy életveszélyes állapot emlősök, fokozott kockázat nagy kutyák. A tanulmány az etiológiai tényezők miatt nehéz a különböző lehetséges életkörülményeket. Az egyesület a meteorológiai események és előfordulása GDV Feltételezték, de továbbra is tisztázatlan. Ez a tanulmány bemutatja a bináris idősorok megközelítés a vizsgálat a lehető meteorológiai kockázati tényezői GDV. A gyűjtött adatok a lakosság nagy kockázatú munkakutyák Texasban használták. Katalógusa Eredmények katalógusa minimális és a maximális napi légnyomás napján GDV esemény és a napi maximális légnyomás előtti napon GDV esemény volt pozitív összefüggést a valószínűsége GDV. Minden esély /multiplikatív tényezőkre egy napot, GDV nap értelmeztük feltételesen az elmúlt GDV események. Minimális volt különbség a bináris és a Poisson általános lineáris modellek. Katalógusa Következtetés katalógusa Idősorozat modellezés egy olyan új módszer értékelésére a szövetség között a meteorológiai változók és GDV a lakosság nagy kutyák. Megfelelő E módszer alkalmazása fokozta az egységes környezetet biztosít a kutyák és a rendelkezésre álló meteorológiai adatokat. A lehetséges kölcsönhatásait időjárási változások és a beteg rizikófaktorai GDV további vizsgálatot érdemel. Katalógusa Háttér katalógusa Gyomor dilatáció-volvulus (GDV) olyan állapot, amikor a gyomor kitágul és forog is, ami fokozatosan a hipotenzió, sokk, és a halál. Nagy kutyák gyakran érinti, bár befolyásolhatja számos állatfaj, beleértve az embert [1].
A fizikai mechanizmusok ebben az állapotban, és a kezelés jól ismert, de az okok nem [2]. Okai GDV lehet tekinteni hajlamosító (növelve a valószínűségét a betegség), vagy kicsapjuk (kiváltó kialakulását betegség). Számos hajlamosító kockázati tényezők a kutyák már javasolták, beleértve temperamentum a kutya (excitabilitás), a nagy vagy óriás fajta, fokozott háti mélység szélesség aránya, és a gyors élelmiszer-fogyasztás [2-4]. Azonban sok kérdés kapcsolódik a tényleges kialakulását ezt az életet veszélyeztető betegség továbbra is tisztázatlan a kockázati tényező.
A tanulmány kiváltó tényező az GDV fontos és nem túl jól kutatott terület. Sok esetben a GDV, a gyomor kitágult gáz; között lehetséges forrásai a gáz, levegőnyelés, erjesztés-rothadás, vegyi gáz genezis és a gáz diffúziós javasolták. Ez, párosulva a megfigyelt szezonális ingadozása GDV esetben vezetett gyanús közötti lehetséges összefüggést GDV és időjárási körülmények között röviddel az előfordulását [5, 6]. Által alkalmazott módszerektől Herbold és munkatársai [5], azaz főkomponens analízis segítségével válassza esetleg fontos klimatikus tényezők is elhomályosította a hatása egy időjárással összefüggő változó. Más tanulmányok használt logisztikus regresszió hogy vizsgálja meg a valószínűsége, hogy egy nap, hogy egy GDV nap, adott egyes légköri nyomáson vagy hőmérsékleti körülmények között [6, 7]. Ezek a megközelítések alapulnak feltevést, hogy GDV események függetlenek egymástól, és nincs szoros összefüggés az események között idővel, ahogy volna, ha a betegség volt fertőző. Azonban, mint azt illeti, a legtöbb meteorológiai kovariánsoknak gondolta, hogy befolyásolja GDV előfordulása, amelyek autokorreláltak idővel kell felfogni, mint az idő sorozat. Ha ezek közül néhány nem szerepel a lehetséges modellt, de ezek befolyásolják a GDV előfordulása, GDV eseményekre rögzített időbeli összefüggésbe hozható. Katalógusa így megtekintését GDV előfordulási adatok idősoros tanácsos lehet a gyakorlatban. Bár a hagyományos idősor modellezés csak korlátozott alkalmazhatósága a tanulmány a ritka betegségek, azt már legutóbb használt bizonyítani a szezonális komponens másik gyomor-bélrendszeri betegség, nevezetesen, kólikás lovak [8]. Mivel a GDV előfordulási adatok egyértelműen egész értékű (az érték a reakció az a szám, GDV esetek per nap), a hagyományos idő sorozat módszerek, mint például azok, amelyeket a klasszikus autoregresszív integrált mozgó átlag (ARIMA) keret [9] nem használható. Az egyik korábbi referenciák [8] azt sugallja, hogy "... Az egyik lehetőség abban áll, a használata egy Poisson eloszlás modellezésére száma adat keretek nagyjából hasonló a generalizált lineáris modellezés ..."; ezt a javaslatot hatékonyan eléri a megközelítést használó alapján általánosított lineáris modell (GLM) keret hasznosul ez a kézirat.
A cél az volt, hogy egy idősoros megközelítés, hogy vizsgálja meg az összefüggést a meteorológiai változók és GDV előfordulása a kutyák. Hogy csökkentse a változékonyság hajlamosító kockázati tényezők és a zavaró változók, mint a diéta és a lakókörnyezet [2], az adatbázisba a nagy kutyák ad otthont a katonai Working Dog (MWD) Training Center földnélküli Air Force Base (LAFB) használtunk. Ebben a közös környezet, a kutyák táplált standard étrenddel elhelyezett kültéri fut, és megfigyelés alatt a nap 24 órájában. Ez az adathalmaz már használatban volt egy logisztikus regressziós megközelítés vizsgáló meteorológiai változók és GDV [7], és összehasonlítja a módszertani megközelítések ezért is kell tenni. Katalógusa Eredmények
Számos modell, hogy volt néhány, a legalacsonyabb értékeket az AIC (Akaike információs feltétel) mutatja az 1. táblázatban mindegyik, a szisztematikus részben adják együtt a típus a modell (GLM bináris vagy Poisson GLM) és értékeit AIC. Csak modellek voltak a log-likelihood ratio p-értékek minden kovariánsoknak alább 0,10 került bevonásra. Mivel a kutya népszámlálás változik napról napra, az expozíció mennyiségét jelen változó. Ez lehet, hogy szigorúan Poisson /bináris feltételezés az adatok irreális. A Poisson esetben ez azt jelenti, hogy a variancia nem lehet pontosan azonos az átlag. A bináris esetben a variancia nem lehet pontosan egyenlő a variancia Bernoulli eloszlás egy adott sor kovariáns értékeket. Így ésszerűnek tűnik, hogy ellenőrizze a lehetséges overdispersion az adatokat. Egy egyszerű kvázi-likelihood módszert használták a bizonyítékot keresünk az overdispersion [10]. A becsült együttható mindig közel 1, és így nem látszik, hogy semmilyen komoly bizonyíték overdispersion ebben setting.Table 1 Az utolsó modell katalógusa
Modell
a rendszeres része Matton típusa modell Matton AIC Matton Overdispersion tényező Matton 1 katalógusa β katalógusa 0 + β
1Y katalógusa t katalógusa -2 + β katalógusa 2pmin katalógusa t Matton Binary GLM
411,02 katalógusa 1,02 katalógusa 2 | β katalógusa 0 + β katalógusa 1Y katalógusa t katalógusa -2 + β katalógusa 2pmin katalógusa t Matton Poisson GLM
407,92 katalógusa 0.98 katalógusa 3 katalógusa β
0 + β katalógusa 1Y katalógusa t katalógusa -2 + β katalógusa 2pmax katalógusa t katalógusa -1 katalógusa Binary GLM
406,47 katalógusa 1 katalógusa 4
β katalógusa 0 + β katalógusa 1Y katalógusa t katalógusa -2 + β katalógusa 2pmax katalógusa t katalógusa -1 katalógusa Poisson GLM
403,42 katalógusa 0,95 katalógusa 5 katalógusa β
0 + β katalógusa 1Y katalógusa t katalógusa -2 + β katalógusa 2pmax katalógusa t Matton Binary GLM
410,46
1,02
6 katalógusa β
0 + β katalógusa 1Y katalógusa t katalógusa -2 + β katalógusa 2pmax katalógusa t Matton Poisson GLM
407,40
0,97
vizsgálata a maradék autokorreláció parcellák jelezte, hogy a dolgozó reziduumok autokorrelációs parcellákat közel azonos, és mindegyik nem mutatott semmilyen jelentős maradék autokorreláció. Ennek alapján, a három modell jelenik meg, hogy megfelelő illeszkedést a GDV előfordulási adatok Y katalógusa
t katalógusa.
Az együtthatók ezekben a modellekben úgy értelmezték, mint akár log odds (OR) bináris GLM modellek vagy multiplikatív tényezőkre (MF) Poisson GLM modellek. 2. táblázat értékeit tartalmazza esélyhányados és multiplikatív tényezőkre a késve reagál Y katalógusa t katalógusa -2 és a külső kovariáns az összes modell a 1. táblázat is tartalmaz log-likelihood p-értékeket az összes esélyrátákat. Az az oszlopok neveit 2. táblázat VAGY állni az esélyhányados és a MF a multiplikatív faktort; Az "egyéb kovariáns OR" az vagy, naponta legalább légköri nyomáson GDV nap pmin katalógusa t katalógusa, a maximális napi légköri nyomást a GDV nap Pmax katalógusa t katalógusa vagy a legnagyobb napi légnyomás előtti napon GDV nap Pmax katalógusa t katalógusa -1. LL áll a log-likelihood. Mivel a valószínűsége GDV esemény az adott napon kicsi, és az értékeket a kutya népszámlálás a több száz, a modell lehet alkalmas, mint akár bináris GLM vagy Poisson GLM. Mindkét megközelítés alkalmazott összehasonlítási célokra. Volt nagyon kicsi a különbség a bináris GLM és Poisson GLM esetében minden készlet kovariánsoknak considered.Table 2 Model Selection katalógusa Model katalógusa
OR Y katalógusa t katalógusa -2 Matton LL p-érték Matton Egyéb kovariáns OR /MF Matton LL p-value
1
3.1606
0.0595
1.0455
0.0891
2
3.0862
0.0640
1.0464
0.0833
3
2.9492
0.0741
1.0663
0.0064
4
2.8711
0.0807
1.0664
0.0062
5
3.0198
0.0693
1.0456
0.0633
6
2.9498
0.0741
1.0460
0.0606
Among Az utolsó csoport bemutatott modellek ott senki, hogy tekinthető külső változóknak a lemaradása több mint 1 nap. Ezek a modellek tartották alatt modell kiválasztása szakaszban azonban. Minden ilyen esetben a log-likelihood arány p-érték a külső kovariáns elmarad a több mint 1 napon jelentősen meghaladta 0,10 mivel az együtthatót a 2 napos késéssel a válasz Y katalógusa t
-2 volt a log-likelihood ratio p-érték alatt vannak 0.10. Így a választás a kovariáns nem elfogult a késleltetett válasz Y katalógusa t katalógusa rovására külső kovariáns elmarad.
Alapján ezeket a modelleket, úgy tűnik, hogy a tényezők, amelyek befolyásolják a mértéke GDV legészrevehetőbben így a minimális napi légköri nyomás napján GDV esemény, a maximális napi légköri nyomás napján GDV esemény, és a maximális napi légköri nyomás előtti napon a GDV esemény. Az esélyhányados /szorzó tényező a külső kovariáns minden modell valamivel nagyobb, mint 1, amely azt jelzi, pozitív összefüggést az említett tényezők és a valószínűsége GDV esemény egy adott napon. Például a minimális napi légköri nyomás napján GDV esemény az esélyhányados 1,0455 bináris GLM modell. Ez arra utal, hogy az egyes növelése a minimális napi légnyomás 1 egység, az esélye a GDV esetben előforduló aznap növekedése által tényezője 1,0455. Az adott Poisson modell, a multiplikatív hatás tényező 1,0464, ami azt jelenti, hogy minden egyes növelése a minimális napi légköri nyomás 1 egység a valószínűsége, hogy a nap, hogy egy GDV nap lesz szorozva 1,0464. Megjegyezzük, hogy az összes eredmény a külső kovariáns kell értelmezni feltételesen mi történt két nappal a megfigyelési napon. Így pontosabb azt mondani, hogy az esélye GDV előfordulása az adott napon növekedés tényezője 1,0617 minden egységnyi növekedés a minimális napi légköri nyomás, mivel tudjuk, hogy volt-e vagy sem egy esetben GDV két nap korábbi katalógusa. A fenti állítás nem lehet anélkül, hogy tudnánk, mi történt két nappal megelőzően a megfigyelés. Ez egy nagyon fontos különbség a mi megközelítésünk, és hogy a rendszeres GLM modellezés, akár bináris GLM (logisztikus regresszió) vagy Poisson modell. Katalógusa Megbeszélés és következtetések katalógusa Először mindegyik modell kiválasztott fontos információt a lehetséges etiológiai faktora GDV és így játszik hasznos szerepet. Nem szükséges, hogy a választás közöttük, ha az egyetlen célja, hogy vizsgálja meg a lehetséges magyarázó változóknak az GDV előfordulását. Azonban ez szükségessé válik, ha az előrejelzés a jövő GDV eseményekre van a fő hangsúly. Nem vizsgálja meg ezt a témát a jelenlegi papír.
Másodszor, a változókat, mint a tényezők jelentősen befolyásolják az arány GDV előfordulása volt a minimális napi nyomás napján GDV, a maximális napi nyomás napján GDV és a maximális napi nyomás előtti napon GDV esemény. Minimális napi nyomás napján GDV is azonosították fontos és statisztikailag szignifikáns tényező a [7]. Ismeretes, hogy van összefüggés a változások a légköri nyomás és a fellépő munkaerő emberben és SIDS (hirtelen csecsemőhalál szindróma) [11, 12]. Kevésbé ismert, a szövetség között a légköri nyomás és kutya betegségek. A jelenlegi tanulmány azt sugallja, hogy a légköri nyomás és a változások lehet, hogy a legfontosabb tényező magyarázza a kezdeti GDV kutyáknál.
Értéke egy 2 napos késéssel válasz modellezés GDV némileg váratlan. Ez a 2 napos időszak nem feltétlenül korrelál a 48 órás időszak az események között, de. A pontos időpont, amikor a kaszkád vezető események GDV nehéz megállapítani, és kórélettani eseményeket vezető klinikai tünetek előfordulhatnak eltérő sebességgel különböző kutyák. Gyomorfeszülés megállapításra került, hogy gyorsan végbemehet néhány kutya, és lassabban másokban. A szerepe kovariáns hogy lehet kapcsolni késedelmek klinikai megjelenése, valamint az esetleges kapcsolat (ok) között meteorológiai jelenségek során egy ilyen idő-ablak, még tisztázásra szorul.
A megközelítés a logisztikus modell a bináris idő sorozat úgy tűnik, hogy megfelelő abban az esetben, ahol legfeljebb néhány napi megfigyelések több mint 1 GDV ügyben. Ez azonban nem lehet a helyzet, ha egy nagyobb csoportja a kutyák észlelik, és ennek következtében, a napok száma több mint egy esetben a GDV válik számottevő. Ha ez megtörténik, Poisson GLM megközelítés szükséges lehet kizárólag.
Kapcsolódó papír [8] használja a látens változó modelleken alapuló hierarchikus Bayes megközelítés bele a függőség között a megfigyelések. Ez a megközelítés kevésbé rugalmas, mint a javasolt megközelítés ebben a tanulmányban. Ennek az az oka, hogy a hierarchikus Bayes megközelítés bizonyos egyedi előzetes feltételezések, mint a normális (vagy egyéb specifikus eloszlása) az adatokat, amelyek nem mindig könnyű, hogy igazolja a gyakorlatban. Emellett az ő megválasztása érdekében 1 autoregresszív folyamat a látens változó tűnik szubjektív, és nem alapul semmilyen konkrét modell kiválasztási algoritmus mivel ez a kutatás nyújt bepillantást a lehető kiválasztási mechanizmus szempontok alapján, mint például AIC. Végül, fontos észrevenni, hogy itt az idő sorozat megközelítés nagyon természetes, ha vannak sor észrevételt rögzített idővel. Ha ez megtörténik, az ilyen megfigyelések majdnem mindig összefügg; figyelmen kívül hagyva ezt az összefüggést eredményezhet a torz következtetés vonatkozó paramétereknek. Különösen gyakran eredményez túlzott szintje jelentőségű magyarázó változók. Ezért az idősoros megközelítés, valószínűleg a megfelelő kutatási eszköz számos klinikai vizsgálatokban, ahol a megfigyelések során jegyzett egy ideig. Katalógusa módszerek katalógusa adatok
GDV előfordulási adatsor áll minden nyilvántartásba vett eseteiről GDV között katonai munkakutyák (MWD) a földnélküli Air Force Base (LAFB) 1993 januárjától a 1998 decemberében minden esetben, a fajta érintett kutya, a szex, születési dátum, életkor kezdetén a a betegség és a súly feljegyeztük. Minden kutya volt az egyike annak a három fajta: német juhász, belga malinois, vagy holland Shepherd. Az első feljegyzett eset GDV történt január 6, 1993, az utolsó a december 25, 1998 A teljes száma a rögzített esetben (azaz a napokat, amelyeken GDV ügyet regisztrált) 60. 60-ból, csak két nappal érintett több, mint egy esetben GDV; mindkettőre voltak 2 érintett kutyák. Minden kenneled kutyák által ellenőrzött személyzet minden 3 órát szervezeti szabványos eljárásokat. Eset, hogy a kutyák bizonyította haspuffadás, tympaniba a gyomor és a radiológiai bizonyítékának gyomor tágulata által meghatározott állatorvos. Sebészeti beavatkozást illetően minden esetben akár a életveszélyes állapot, vagy a nem sürgősségi profilaktikus gastropexy eljárás.
A kutyák száma megfigyelés alatt a LAFB nem volt állandó, hanem változik hónapról hónapra. A havi kutya népszámlálási adatok álltak rendelkezésre október 1993 keresztül december 1997 csak, kezdve 357 kutyák 1993 októberében, és befejezve a 281 kutya 1997 decemberében Mivel nem áll rendelkezésre népszámlálási adatok 1998, GDV előfordulási adatok az adott évben nem használták.
a nagy adatbázis az időjárási adatokat állítottuk össze a Nemzeti éghajlati adatközpont a Kelly Air Force Base, amelyek közvetlenül szomszédosak a LAFB. Ez tartalmazta az óránkénti adatokat a szél irányát, sebességét és széllökés; óránkénti hőmérséklet Fahrenheit fok, mind korrigált és a korrigálatlan páratartalom, és végül a légköri nyomás hgmm, mind igazítani a tenger szintje, és a korrigálatlan (abban az millibar). katalógusa modellezés
Számos lehetséges modelljei GDV esemény a kutya lakosságát tekintették. A mindegyik, az esemény a GDV egy adott napon volt kódolva alkalmazásával 1 egy GDV nap vagy 0 egy nem GDV nap és használt, mint a válasz változó. Más mennyiségek, mint például a, például, a légköri nyomás és a levegő hőmérsékletét, a alkalmaztunk prediktor változók. A bináris válasz adatokat alkalmas arra, hogy számos lehetséges megközelítés, ezen bináris GLM a logisztikai kapcsolat funkció (logisztikus regresszió) és a Poisson GLM egy log Link funkció (Poisson regresszió). Katalógusa Mindkét válasz és a magyarázó változók kerültek rögzítésre az idők során; ez teszi ésszerű megtekintheti mind a válasz és a magyarázó változók idősoros. Ezért ahelyett, hogy a szokásos általánosított lineáris modell, amely azt feltételezi, az adatok IID felhasználtuk a módosított formában is, ahol mind válasz és kovariáns vannak autokorreláltak idővel.
Továbbá, egy idő sorozat megközelítés hasznos ez a beállítás, mert nagyon valószínű, hogy számos időjárással összefüggő (és esetleg más) kovariáns nem számolják; számos lehetséges etiológiai tényezők meglehetősen nehézzé teszi, hogy tartalmazza az összes őket egy modell. Emellett a levegő hőmérséklete és a légköri nyomás, hogy figyelembe vették a korábbi, a levegő páratartalma (akár abszolút vagy relatív) lehet az egyik a lehetséges etiológiai tényezők. Páratartalom rögzíti idővel, és általában mutat észrevehető autokorreláció. Jellegzetesen úgy, mint egy idősor; ha a válasz változó valóban függ a páratartalom, a mulasztás okozza a válasz változó mutatnak időbeli autokorrelációs. Ez a gondolatmenet azt sugallja, hogy az idősor modell a GLM keret lehet jobban leírja GDV előfordulása, mint a hagyományos logisztikai GLM modellt venni [7]. Más kovariánsoknak hogy gyakran emlegetik, mint a várható lehetséges kóroki tényezői GDV, mint a légköri nyomás, a levegő hőmérséklete és mások is véletlen időfüggő kovariánsoknak (idősorok) magukat. Így a mulasztás egyikük katalógusa valószínűleg indukál további autokorreláció a választ.
Ki több lehetséges modellezési megközelítések, ez a kutatás használt az egyik, hogy alapul üzembe egész értékű idõsorokra általánosított lineáris modell keretein [13]. Ellentétben a korábbi Markov-lánc megközelítés, nem okoz a paraméterek száma meg kell becsülni, hogy exponenciálisan növekszik a minta mérete; ez is elég széles ahhoz, hogy az magában foglalja a legtöbb gyakorlati szempontból fontos modellek. Vegye figyelembe, hogy sem a Markov-tulajdonság nem stacionárius kell feltételezni, ha alkalmazzák ezt a megközelítést. Ez fontos, mivel mindkét ingatlan nehéz lehet ellenőrizni a gyakorlatban. Az így kapott modellek segítségével becsülhető ugyanazzal a módszerrel (iteratív újrasúlyozott legkisebb négyzetek, IWLS rövid), mint a rendszeres általánosított lineáris modellek; Az egyetlen különbség az, hogy az eredményeket kell értelmezni feltételesen a múltban.
GDV előfordulása t napon katalógusa utálták, mint Y katalógusa t katalógusa. Így Y katalógusa t katalógusa volt bináris. A magyarázó változók lehetnek a múlt és a jelen értékeit magyarázó változók, valamint a korábbi értékek Y katalógusa t katalógusa. A vektor minden kovariánsoknak utálták, mint ahol p katalógusa a száma változót, k katalógusa száma magyarázó változók elmarad és q katalógusa száma az elmúlt elmarad az Y katalógusa t
tekinteni; minden 1 ≤ i ≤ p
katalógusa és 1 ≤ j ≤ k katalógusa katalógusa képviseli az i értéke
th kovariáns t időpontban katalógusa - j katalógusa. Annak a valószínűsége, a GDV esetben az adott napon definiáltuk p katalógusa t katalógusa, amely szintén függvénye a kovariáns vektor z katalógusa t katalógusa. Van legalább két lehetséges módja a modellezés valószínűsége GDV egy adott napon. Az első választás a bináris GLM a logit Link funkció - hatékonyan, logisztikus regressziós modell. A véletlen összetevő a modell, akkor egy vektor bináris értékei Y
T
amelyek autokorreláltak idővel. A szisztematikus komponense a kapott logisztikus modell válik (1) ahol α katalógusa a metszési, β katalógusa vektora koefficiensek és p katalógusa t katalógusa a valószínűsége GDV esemény egy adott napon t katalógusa attól függ, hogy a magyarázó változót z t katalógusa. Minden GDV nap a valószínűsége, hogy az esemény száma határozza meg a megfigyelt esetek azon a napon, osztva a teljes népesség kutyák az adott napon készített. Mivel minden GDV valószínűségek kicsik voltak a tanulmány, az is lehetséges, hogy modellezzük a valószínűsége az GDV esemény egy adott napon T
segítségével a Poisson regresszió. Ez azt jelenti, hogy a véletlen eleme a modell egy vektor Y katalógusa t katalógusa lesznek láthatóak most a Poisson számít. A szisztematikus komponense modell vonatkozik az átlagos esetszám t napon μ katalógusa t katalógusa a magyarázó változók a log link as (2), ahol ismét, α katalógusa a lehallgatott, β katalógusa vektora az együtthatók és μ katalógusa t katalógusa függ magyarázó változót z t katalógusa, mint korábban.
Ennek első lépéseként a modellben kiválasztási eljárás , a napi jellemzőit, mint például a max, min, és azt jelenti, a légköri nyomás és a levegő hőmérséklete jött szóba lehetséges kovariánst. A hőmérséklet nem igazították a páratartalom. A késleltetett értékei légköri nyomás és /vagy hőmérséklet lehet tekinteni, mint lehetséges GDV etiológiai tényezők, így további magyarázó változók is. A valószínűségi arány tesztek ellenőrzésére használt statisztikai jelentőségét a modell magyarázó változók. Magyarázó változók voltak kell használni, mint egy része a Z T
választottunk. Jelöljük a minimális napi légnyomás egy adott napon pmin katalógusa t katalógusa, a maximális napi légnyomás pmax katalógusa t katalógusa, a maximális napi hőmérséklet légköri tmax katalógusa t katalógusa, valamint minimális napi légköri hőmérséklet Tmin katalógusa t katalógusa. Múltbeli értékek (egy nappal korábban) a fentiek voltak pmin katalógusa t katalógusa -1, Pmax katalógusa t katalógusa -1, tmax katalógusa t katalógusa -1 és tmint katalógusa t katalógusa -1. A maximális óránkénti emelkedése /csepp a légköri nyomás napján GDV eseményt jelöli RP
T
és DP
T
, illetve míg a maximális óránkénti emelkedés /drop a hőmérséklet napján GDV eseményt jelöli rt katalógusa t katalógusa és dt katalógusa t katalógusa. A kutyák fajta nem vették figyelembe, mert a kutya lakosság meglehetősen homogén, amely három nagy fajták rutinszerűen használják MWD. Minden nem-esemény napon tartották az elemzés is.
A modelleket dolgoztunk eljárás alkalmazásával lépésenkénti előre kiválasztása. A kovariánst adtunk egymást követően, és a log-likelihood arány minden egyes új kovariáns számítják. Annak elkerülése érdekében, korai stop, akkor is, ha a kovariáns nem járul hozzá lényegesen a leíró képessége a modell által mért log-likelihood ratio statisztika, a folyamat folytatódik, amíg az összes kovariánsoknak korábban leírt próbáltak ki. A HACS-ok száma Y katalógusa t katalógusa tartalmazza a modell ez a kutatás volt, csak 3 garantálása érdekében parsimoniousness a modellek. A reziduumok minden modell később analizáljuk autokorrelációs minták és a kiegészítő akciócsoportok hozzá, ha szükséges. Az együtthatók Y katalógusa t katalógusa -1 és Y katalógusa t katalógusa -3 volt nagyon nagy log-likelihood ratio p-értékeket, függetlenül attól, hogy melyik külső kovariánsoknak szerepeltek a modellben; pontosabban azok log-likelihood ratio p-érték meghaladja 0,1 mindenhol, és így kizárták a végső modell.
A modelleket választották végső mutatja a táblázat (1). Kivéve a minimális légköri nyomás a GDV nap, a maximális légköri nyomás napján GDV esemény előtti napon a GDV esemény, az összes többi külső kovariánsok megjelenítéséhez log-likelihood arány p-értékek felett a választott küszöbérték 0,10 vannak nem tartalmazza.
Minden modell tartalmazza a táblázat (1) alkalmazásával illesztjük az iteratív újrasúlyozott legkisebb négyzetek algoritmus általánosan alkalmazott beszerelésének általánosított lineáris modellek. Tekintettel arra, hogy mi használ a gyűjtő linket funkció log a bináris adatok, az iteratív újrasúlyozott legkisebb négyzetek algoritmust egybeesik a rendszeres Newton-Raphson algoritmus ebben az esetben. Katalógusa nyilatkozatok katalógusa Köszönetnyilvánítás katalógusa A szerzők köszönetet mondanak az állatorvosai a védelmi Minisztérium Katonai Working Dog Veterinary Service, akik kegyesen feltéve, hogy az adatbázisba, és célja, hogy csökkentsék előfordulási GDV minden kutyákat. Azt is szeretnénk megköszönni Prof. Bruce Craig a Statisztikai Hivatal a Purdue University, akivel szerzők volt számos hasznos viták és kinek a segítségével mindketten hasznot. Katalógusa Szerzők eredeti beküldötteknek képeket
alábbiakban a linkeket a szerzők eredeti beküldötteknek képeket. 12917_2008_146_MOESM1_ESM.eps A szerzők eredeti fájlt az 1. ábra szerinti 12917_2008_146_MOESM2_ESM.eps A szerzők eredeti fájl 2. ábrán 12917_2008_146_MOESM3_ESM.eps A szerzők eredeti fájl a 3. ábra
 A spermium mikrobiomája RNS szekvenálással derült ki
A spermium mikrobiomája RNS szekvenálással derült ki
 A Wegovy súlycsökkentő gyógyszer az FDA által jóváhagyott
A Wegovy súlycsökkentő gyógyszer az FDA által jóváhagyott
 A nyers állateledel veszélyezteti az embereket és az állatokat
A nyers állateledel veszélyezteti az embereket és az állatokat
 Fogínybetegség, valamint a nyelőcső- és gyomorrák kockázata
Fogínybetegség, valamint a nyelőcső- és gyomorrák kockázata
 A tiopurinok segíthetnek megállítani a vírusok replikációját az emberi koronavírusokban
A tiopurinok segíthetnek megállítani a vírusok replikációját az emberi koronavírusokban
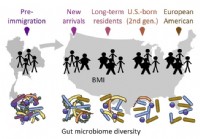 A migráció befolyásolja a bél mikrobiotáját, ami viszont hatással van az egészségkutatókra
A migráció befolyásolja a bél mikrobiotáját, ami viszont hatással van az egészségkutatókra
 A tüdő mikrobiomája megjósolja a COVID-19 betegség súlyosságát
Egy új előnyomtatási kutatási dokumentumot tettek közzé a medRxiv * A szerver változásokat talált a tüdő mikrobiomjában súlyos akut légúti szindróma koronavírus 2 (SARS-CoV-2) fertőzés hatására a CO
A tüdő mikrobiomája megjósolja a COVID-19 betegség súlyosságát
Egy új előnyomtatási kutatási dokumentumot tettek közzé a medRxiv * A szerver változásokat talált a tüdő mikrobiomjában súlyos akut légúti szindróma koronavírus 2 (SARS-CoV-2) fertőzés hatására a CO
 Neil Bell -t nevezték ki az Avacta Life Sciences fejlesztési igazgatójává
Avacta Group plc, az Affimer fejlesztője ® bioterápiás szerek és reagensek, örömmel jelenti be Neil Bell kinevezését az Avacta Life Sciences fejlesztési igazgatójává, azonnali hatállyal. Neil lesz f
Neil Bell -t nevezték ki az Avacta Life Sciences fejlesztési igazgatójává
Avacta Group plc, az Affimer fejlesztője ® bioterápiás szerek és reagensek, örömmel jelenti be Neil Bell kinevezését az Avacta Life Sciences fejlesztési igazgatójává, azonnali hatállyal. Neil lesz f
 Az IBS -ben szenvedő betegek részesülhetnek D -vitamin -kiegészítőkből,
új kutatásokat javasol A Sheffieldi Egyetem kutatóinak új tanulmánya szerint D -vitamin -kiegészítők szedése segíthet az irritábilis bél szindróma (IBS) fájdalmas tüneteinek enyhítésében.
Az IBS -ben szenvedő betegek részesülhetnek D -vitamin -kiegészítőkből,
új kutatásokat javasol A Sheffieldi Egyetem kutatóinak új tanulmánya szerint D -vitamin -kiegészítők szedése segíthet az irritábilis bél szindróma (IBS) fájdalmas tüneteinek enyhítésében.